
Question Number 105700 by john santu last updated on 31/Jul/20
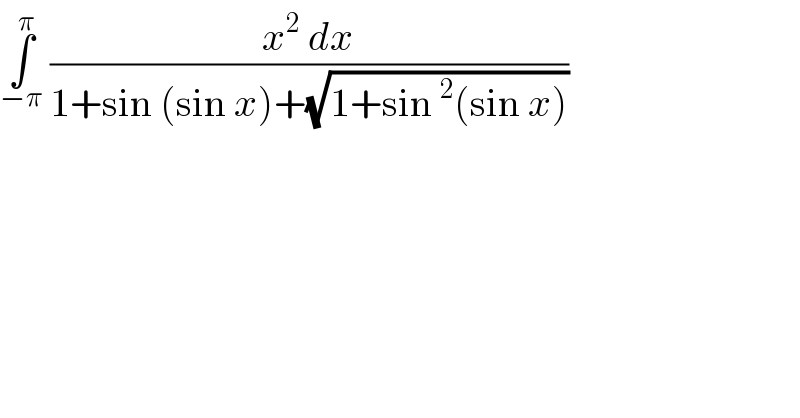
$$\underset{−\pi} {\overset{\pi} {\int}}\:\frac{{x}^{\mathrm{2}} \:{dx}}{\mathrm{1}+\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}} \\ $$$$ \\ $$
Answered by bramlex last updated on 31/Jul/20

$${I}=\:\underset{−\pi} {\overset{\pi} {\int}}\:\frac{{x}^{\mathrm{2}} {dx}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}+\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$${replace}\:{x}\:{by}\:−{x} \\ $$$${I}=\underset{\pi} {\overset{−\pi} {\int}}\frac{{x}^{\mathrm{2}} \left(−{dx}\right)}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}−\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$${I}=\underset{−\pi} {\overset{\pi} {\int}}\frac{{x}^{\mathrm{2}} {dx}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}−\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$\mathrm{2}{I}=\underset{−\pi} {\overset{\pi} {\int}}\:\frac{\mathrm{2}{x}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}\right)\:{dx}}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}\right)} \\ $$$$\mathrm{2}{I}=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}\right)}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:{x}\right)}\right)}\:{dx} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\:{x}^{\mathrm{2}} \:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\pi^{\mathrm{3}} \:.\bigstar \\ $$
