
Question Number 105686 by bramlex last updated on 31/Jul/20
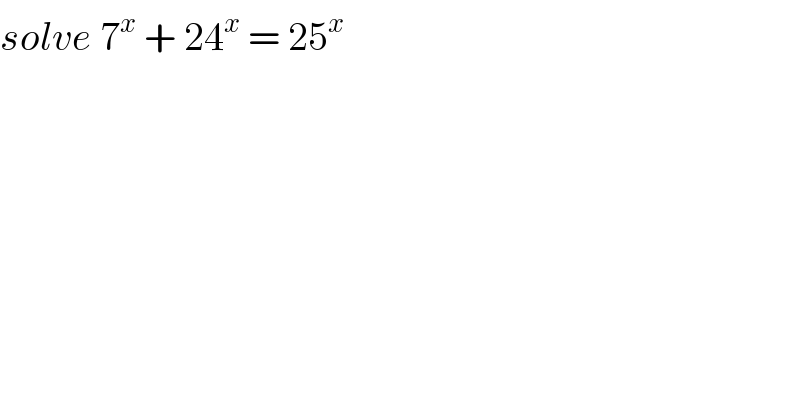
$${solve}\:\mathrm{7}^{{x}} \:+\:\mathrm{24}^{{x}} \:=\:\mathrm{25}^{{x}} \: \\ $$
Answered by Rasheed.Sindhi last updated on 31/Jul/20

$$\left(\frac{\mathrm{7}}{\mathrm{25}}\right)^{{x}} +\left(\frac{\mathrm{24}}{\mathrm{25}}\right)^{{x}} =\mathrm{1} \\ $$$${Let}\:\frac{\mathrm{7}}{\mathrm{25}}=\mathrm{sin}\:\theta, \\ $$$$\:\:\:\mathrm{cos}\:\theta=\sqrt{\mathrm{1}−\mathrm{si}{n}^{\mathrm{2}} \theta}=\sqrt{\mathrm{1}−\left(\frac{\mathrm{7}}{\mathrm{25}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\sqrt{\mathrm{1}−\frac{\mathrm{49}}{\mathrm{625}}}\:=\sqrt{\frac{\mathrm{625}−\mathrm{49}}{\mathrm{625}}}=\frac{\mathrm{24}}{\mathrm{25}} \\ $$$$\therefore\:\left(\frac{\mathrm{7}}{\mathrm{25}}\right)^{{x}} +\left(\frac{\mathrm{24}}{\mathrm{25}}\right)^{{x}} =\mathrm{1}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{sin}\:\theta\right)^{{x}} +\left(\mathrm{cos}\:\theta\right)^{{x}} =\mathrm{1} \\ $$$${Comparing}\:{with}\:{the}\:{identity}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\left(\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{2} \\ $$
Commented by bramlex last updated on 31/Jul/20

$${cooll}\:\&\:{jooss} \\ $$
