
Question Number 105616 by DeepakMahato last updated on 30/Jul/20
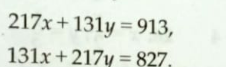
Answered by nimnim last updated on 30/Jul/20
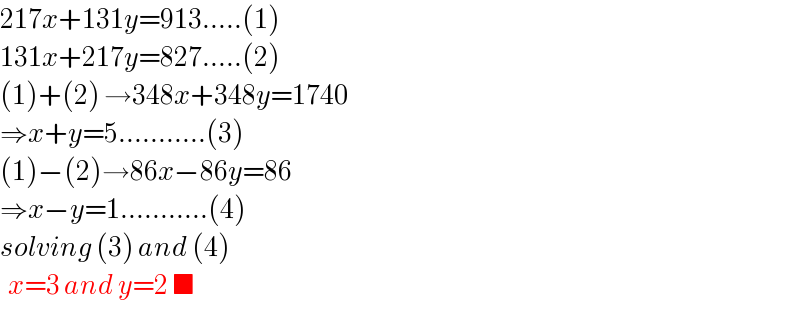
$$\mathrm{217}{x}+\mathrm{131}{y}=\mathrm{913}.....\left(\mathrm{1}\right) \\ $$$$\mathrm{131}{x}+\mathrm{217}{y}=\mathrm{827}.....\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:\rightarrow\mathrm{348}{x}+\mathrm{348}{y}=\mathrm{1740} \\ $$$$\Rightarrow{x}+{y}=\mathrm{5}...........\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\rightarrow\mathrm{86}{x}−\mathrm{86}{y}=\mathrm{86} \\ $$$$\Rightarrow{x}−{y}=\mathrm{1}...........\left(\mathrm{4}\right) \\ $$$${solving}\:\left(\mathrm{3}\right)\:{and}\:\left(\mathrm{4}\right) \\ $$$$\:\:{x}=\mathrm{3}\:{and}\:{y}=\mathrm{2}\:\blacksquare \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jul/20

$$\mathcal{G}{ood}! \\ $$
Commented by nimnim last updated on 30/Jul/20

$${Thank}\:{you}\:{Sir}. \\ $$
Commented by DeepakMahato last updated on 31/Jul/20

$${Thank}\:{you} \\ $$
Answered by 1549442205PVT last updated on 30/Jul/20

$$\mathrm{D}=\begin{vmatrix}{\mathrm{217}}&{\mathrm{132}}\\{\mathrm{131}}&{\mathrm{217}}\end{vmatrix}=\mathrm{217}^{\mathrm{2}} −\mathrm{131}^{\mathrm{2}} =\mathrm{186}=\mathrm{29928} \\ $$$$\mathrm{D}_{\mathrm{x}} =\begin{vmatrix}{\mathrm{913}}&{\mathrm{131}}\\{\mathrm{827}}&{\mathrm{217}}\end{vmatrix}=\mathrm{913}.\mathrm{217}−\mathrm{827}.\mathrm{131}=\mathrm{89784} \\ $$$$\mathrm{x}=\frac{\mathrm{D}_{\mathrm{x}} }{\mathrm{D}_{\mathrm{y}} }=\frac{\mathrm{89784}}{\mathrm{29928}}=\mathrm{3} \\ $$$$\mathrm{D}_{\mathrm{y}} =\begin{vmatrix}{\mathrm{217}}&{\mathrm{913}}\\{\mathrm{131}}&{\mathrm{827}}\end{vmatrix}=\mathrm{217}.\mathrm{827}−\mathrm{913}.\mathrm{131}=\mathrm{59856} \\ $$$$\mathrm{y}=\frac{\mathrm{D}_{\mathrm{y}} }{\mathrm{D}}=\frac{\mathrm{59856}}{\mathrm{29928}}=\mathrm{2} \\ $$
