
Question Number 105594 by ajfour last updated on 30/Jul/20
Commented by ajfour last updated on 30/Jul/20
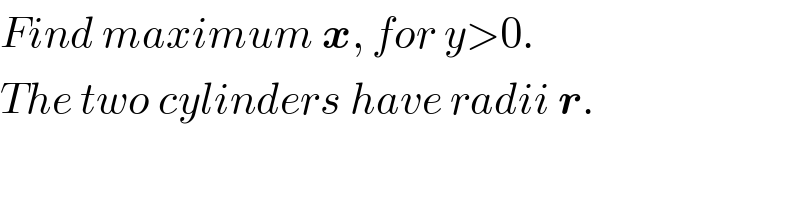
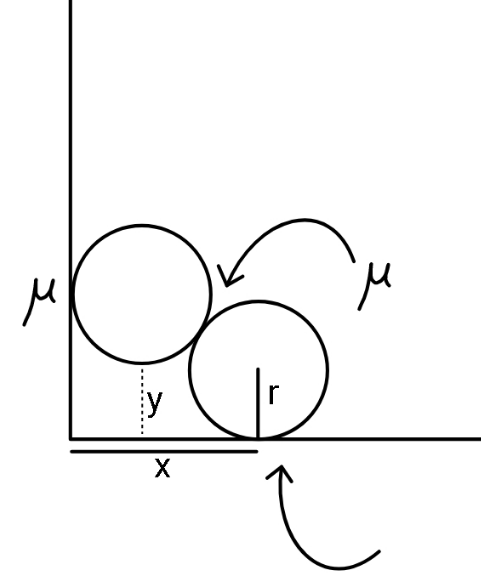
$${Find}\:{maximum}\:\boldsymbol{{x}},\:{for}\:{y}>\mathrm{0}. \\ $$$${The}\:{two}\:{cylinders}\:{have}\:{radii}\:\boldsymbol{{r}}. \\ $$
Commented by ajfour last updated on 30/Jul/20
Commented by ajfour last updated on 30/Jul/20
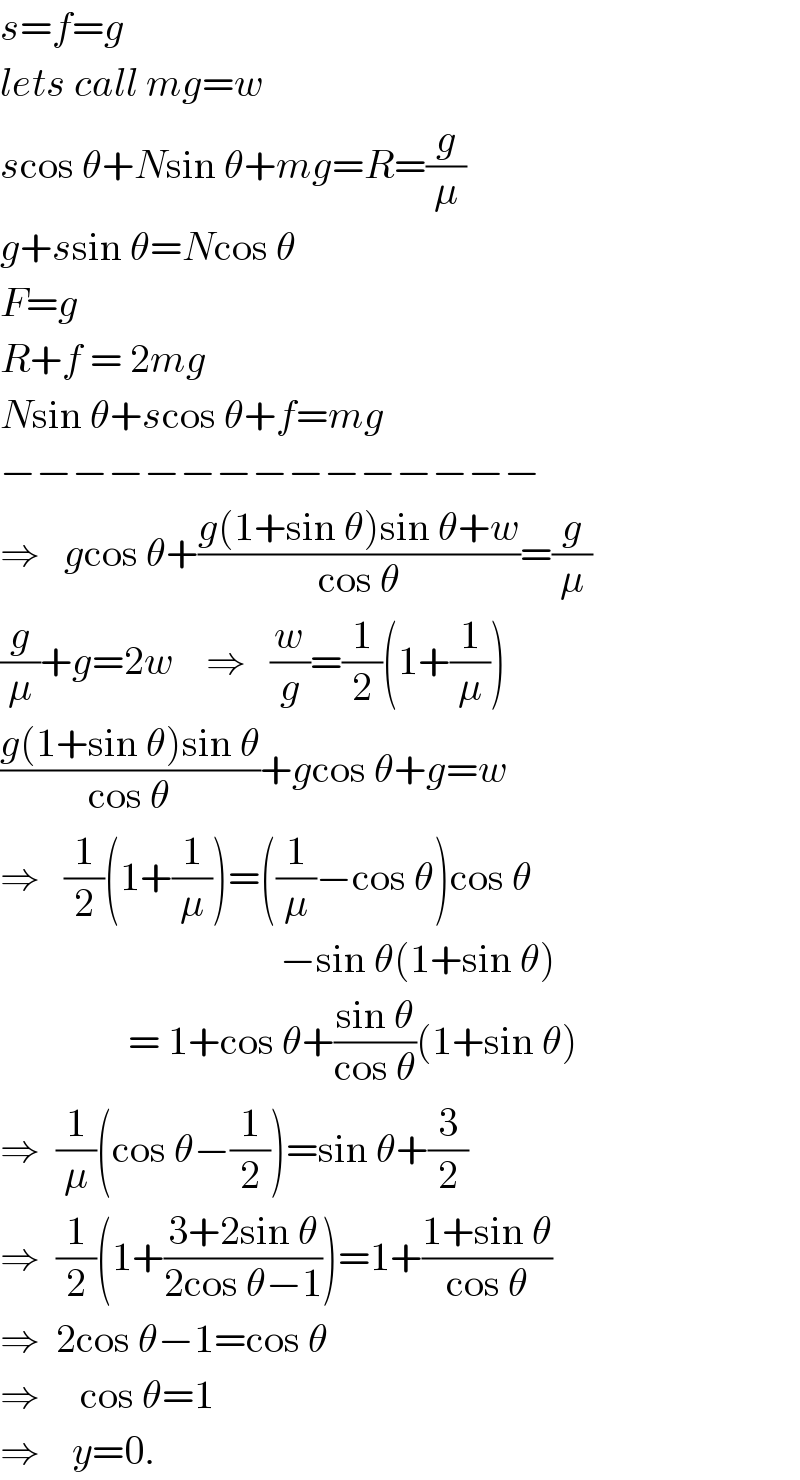
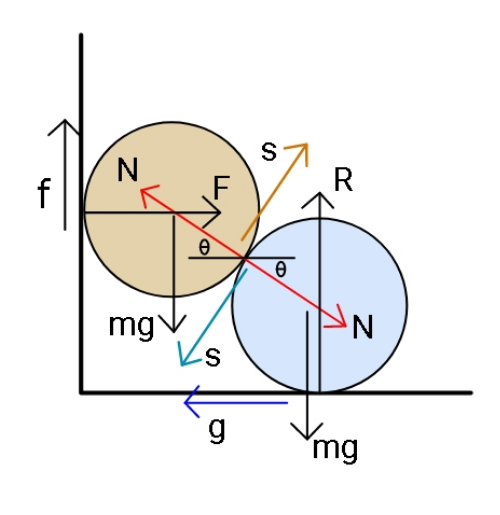
$${s}={f}={g} \\ $$$${lets}\:{call}\:{mg}={w} \\ $$$${s}\mathrm{cos}\:\theta+{N}\mathrm{sin}\:\theta+{mg}={R}=\frac{{g}}{\mu} \\ $$$${g}+{s}\mathrm{sin}\:\theta={N}\mathrm{cos}\:\theta \\ $$$${F}={g} \\ $$$${R}+{f}\:=\:\mathrm{2}{mg} \\ $$$${N}\mathrm{sin}\:\theta+{s}\mathrm{cos}\:\theta+{f}={mg} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\Rightarrow\:\:\:{g}\mathrm{cos}\:\theta+\frac{{g}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\mathrm{sin}\:\theta+{w}}{\mathrm{cos}\:\theta}=\frac{{g}}{\mu} \\ $$$$\frac{{g}}{\mu}+{g}=\mathrm{2}{w}\:\:\:\:\Rightarrow\:\:\:\frac{{w}}{{g}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mu}\right) \\ $$$$\frac{{g}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}+{g}\mathrm{cos}\:\theta+{g}={w} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mu}\right)=\left(\frac{\mathrm{1}}{\mu}−\mathrm{cos}\:\theta\right)\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{sin}\:\theta\left(\mathrm{1}+\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\left(\mathrm{1}+\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mu}\left(\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{sin}\:\theta+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{3}+\mathrm{2sin}\:\theta}{\mathrm{2cos}\:\theta−\mathrm{1}}\right)=\mathrm{1}+\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\:\:\mathrm{2cos}\:\theta−\mathrm{1}=\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{cos}\:\theta=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:{y}=\mathrm{0}. \\ $$
