
Question Number 105504 by bemath last updated on 29/Jul/20
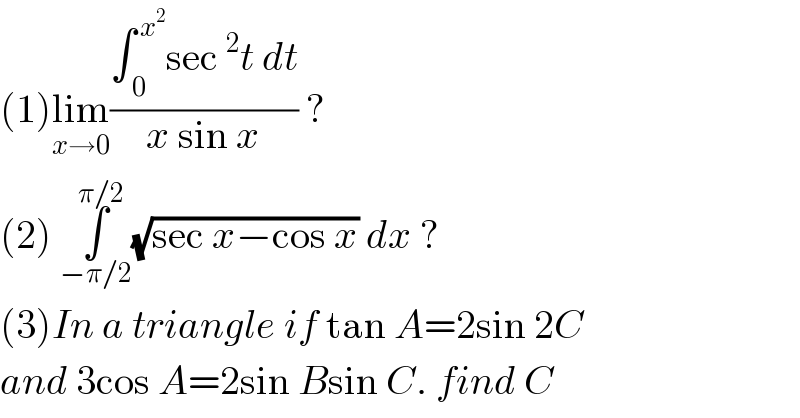
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\int_{\:\mathrm{0}} ^{\:{x}^{\mathrm{2}} } \mathrm{sec}\:^{\mathrm{2}} {t}\:{dt}}{{x}\:\mathrm{sin}\:{x}}\:? \\ $$$$\left(\mathrm{2}\right)\:\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\sqrt{\mathrm{sec}\:{x}−\mathrm{cos}\:{x}}\:{dx}\:? \\ $$$$\left(\mathrm{3}\right){In}\:{a}\:{triangle}\:{if}\:\mathrm{tan}\:{A}=\mathrm{2sin}\:\mathrm{2}{C} \\ $$$${and}\:\mathrm{3cos}\:{A}=\mathrm{2sin}\:{B}\mathrm{sin}\:{C}.\:{find}\:{C} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Jul/20
![1)lim_(x→0) ((∫_0 ^x^2 sec^2 tdt)/(xsinx))=lim_(x→0) (([tan t]_0 ^x^2 )/x^2 ) { sinx→x =lim_(x→0) ((tan x^2 )/x^2 )=1](Q105505.png)
$$\left.\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} } {sec}^{\mathrm{2}} {tdt}}{{xsinx}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[{tan}\:{t}\right]_{\mathrm{0}} ^{{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\:\:\:\:{sinx}\rightarrow{x}\right. \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{tan}\:{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=\mathrm{1} \\ $$
Answered by john santu last updated on 29/Jul/20
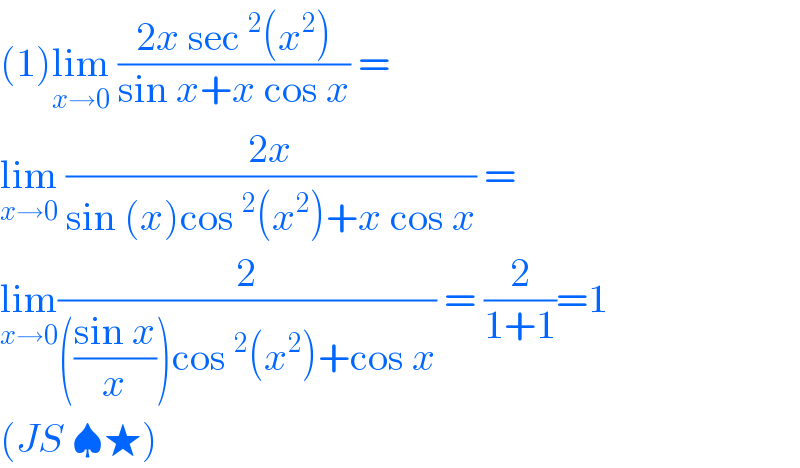
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}\:\mathrm{sec}\:^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)}{\mathrm{sin}\:{x}+{x}\:\mathrm{cos}\:{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}}{\mathrm{sin}\:\left({x}\right)\mathrm{cos}\:^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)+{x}\:\mathrm{cos}\:{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}}{\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)\mathrm{cos}\:^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)+\mathrm{cos}\:{x}}\:=\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{1}}=\mathrm{1} \\ $$$$\left({JS}\:\spadesuit\bigstar\right) \\ $$
Answered by Ar Brandon last updated on 29/Jul/20
![1\lim_(x→0) ((∫_0 ^x^2 sec^2 tdt)/(xsinx))=lim_(x→0) (([tanx]_0 ^x^2 )/(xsinx))=lim_(x→0) ((tanx^2 )/(xsinx)) =lim_(x→0) (x^2 /(xsinx))=lim_(x→0) (x/(sinx))=lim_(x→0) (1/(cosx))=1](Q105510.png)
$$\mathrm{1}\backslash\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \mathrm{sec}^{\mathrm{2}} \mathrm{tdt}}{\mathrm{xsinx}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[\mathrm{tanx}\right]_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } }{\mathrm{xsinx}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tanx}^{\mathrm{2}} }{\mathrm{xsinx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{xsinx}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}}{\mathrm{sinx}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{cosx}}=\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Jul/20
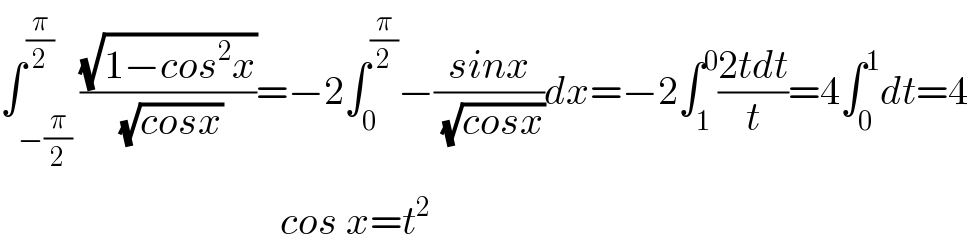
$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} {x}}}{\sqrt{{cosx}}}=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\frac{{sinx}}{\sqrt{{cosx}}}{dx}=−\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{2}{tdt}}{{t}}=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {dt}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cos}\:{x}={t}^{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jul/20
Hey Brandon sir , can you take a try on my question?�� Question no 105498
Commented by Ar Brandon last updated on 29/Jul/20
��OK bro, but I'm not Sir. Next 2 years I'll be thrice as old as I was e^2.3 years ago to the nearest round figure.��
Commented by Dwaipayan Shikari last updated on 29/Jul/20
����������My current age is e^2.79
Commented by Dwaipayan Shikari last updated on 29/Jul/20
A high school one
Commented by Ar Brandon last updated on 29/Jul/20
��
Answered by Ar Brandon last updated on 29/Jul/20
![I=∫_(−(π/2)) ^(π/2) (√(secx−cosx))dx=2∫_0 ^(π/2) (√((1−cos^2 x)/(cosx)))dx=2∫_0 ^(π/2) ((sinx)/(√(cosx)))dx =−2∫_0 ^(π/2) ((d(cosx))/(√(cosx)))=−4[(√(cosx))]_0 ^(π/2) =4](Q105519.png)
$$\mathcal{I}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{secx}−\mathrm{cosx}}\mathrm{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}}}\mathrm{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}}{\sqrt{\mathrm{cosx}}}\mathrm{dx} \\ $$$$\:\:\:=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{d}\left(\mathrm{cosx}\right)}{\sqrt{\mathrm{cosx}}}=−\mathrm{4}\left[\sqrt{\mathrm{cosx}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{4} \\ $$
Answered by mathmax by abdo last updated on 29/Jul/20
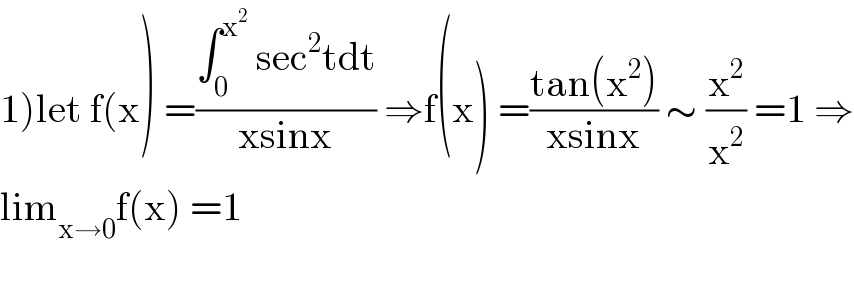
$$\left.\mathrm{1}\right)\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \:\mathrm{sec}^{\mathrm{2}} \mathrm{tdt}}{\mathrm{xsinx}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{tan}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{xsinx}}\:\sim\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 29/Jul/20
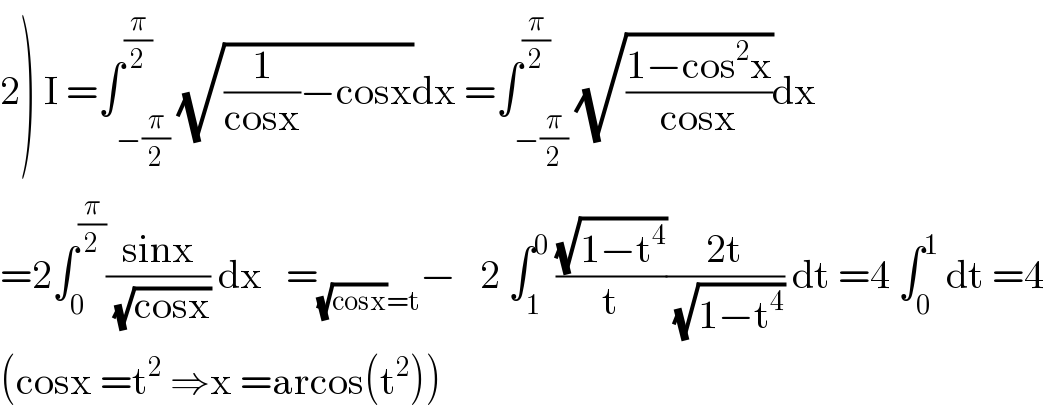
$$\left.\mathrm{2}\right)\:\mathrm{I}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}}{\mathrm{cosx}}−\mathrm{cosx}}\mathrm{dx}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}}}\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}}{\sqrt{\mathrm{cosx}}}\:\mathrm{dx}\:\:\:=_{\sqrt{\mathrm{cosx}}=\mathrm{t}} −\:\:\:\mathrm{2}\:\int_{\mathrm{1}} ^{\mathrm{0}} \:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }}{\mathrm{t}}\frac{\mathrm{2t}}{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }}\:\mathrm{dt}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{dt}\:=\mathrm{4} \\ $$$$\left(\mathrm{cosx}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\mathrm{arcos}\left(\mathrm{t}^{\mathrm{2}} \right)\right) \\ $$
Answered by bramlex last updated on 29/Jul/20
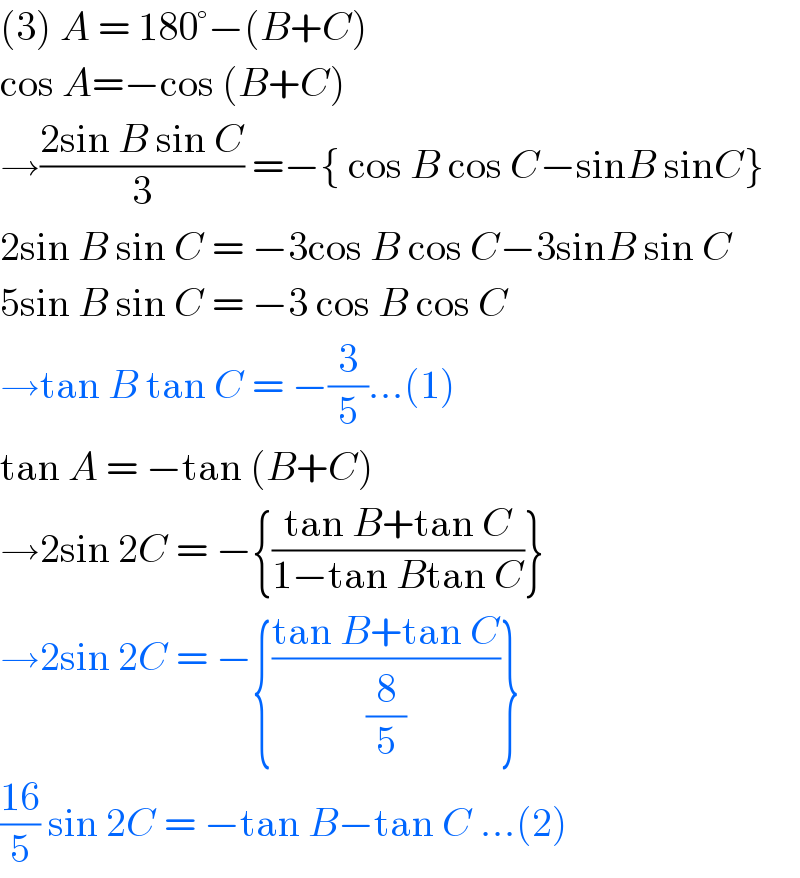
$$\left(\mathrm{3}\right)\:{A}\:=\:\mathrm{180}°−\left({B}+{C}\right) \\ $$$$\mathrm{cos}\:{A}=−\mathrm{cos}\:\left({B}+{C}\right) \\ $$$$\rightarrow\frac{\mathrm{2sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{3}}\:=−\left\{\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}−\mathrm{sin}{B}\:\mathrm{sin}{C}\right\} \\ $$$$\mathrm{2sin}\:{B}\:\mathrm{sin}\:{C}\:=\:−\mathrm{3cos}\:{B}\:\mathrm{cos}\:{C}−\mathrm{3sin}{B}\:\mathrm{sin}\:{C} \\ $$$$\mathrm{5sin}\:{B}\:\mathrm{sin}\:{C}\:=\:−\mathrm{3}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C} \\ $$$$\rightarrow\mathrm{tan}\:{B}\:\mathrm{tan}\:{C}\:=\:−\frac{\mathrm{3}}{\mathrm{5}}...\left(\mathrm{1}\right) \\ $$$$\mathrm{tan}\:{A}\:=\:−\mathrm{tan}\:\left({B}+{C}\right) \\ $$$$\rightarrow\mathrm{2sin}\:\mathrm{2}{C}\:=\:−\left\{\frac{\mathrm{tan}\:{B}+\mathrm{tan}\:{C}}{\mathrm{1}−\mathrm{tan}\:{B}\mathrm{tan}\:{C}}\right\} \\ $$$$\rightarrow\mathrm{2sin}\:\mathrm{2}{C}\:=\:−\left\{\frac{\mathrm{tan}\:{B}+\mathrm{tan}\:{C}}{\frac{\mathrm{8}}{\mathrm{5}}}\right\} \\ $$$$\frac{\mathrm{16}}{\mathrm{5}}\:\mathrm{sin}\:\mathrm{2}{C}\:=\:−\mathrm{tan}\:{B}−\mathrm{tan}\:{C}\:...\left(\mathrm{2}\right) \\ $$
Answered by Ar Brandon last updated on 29/Jul/20
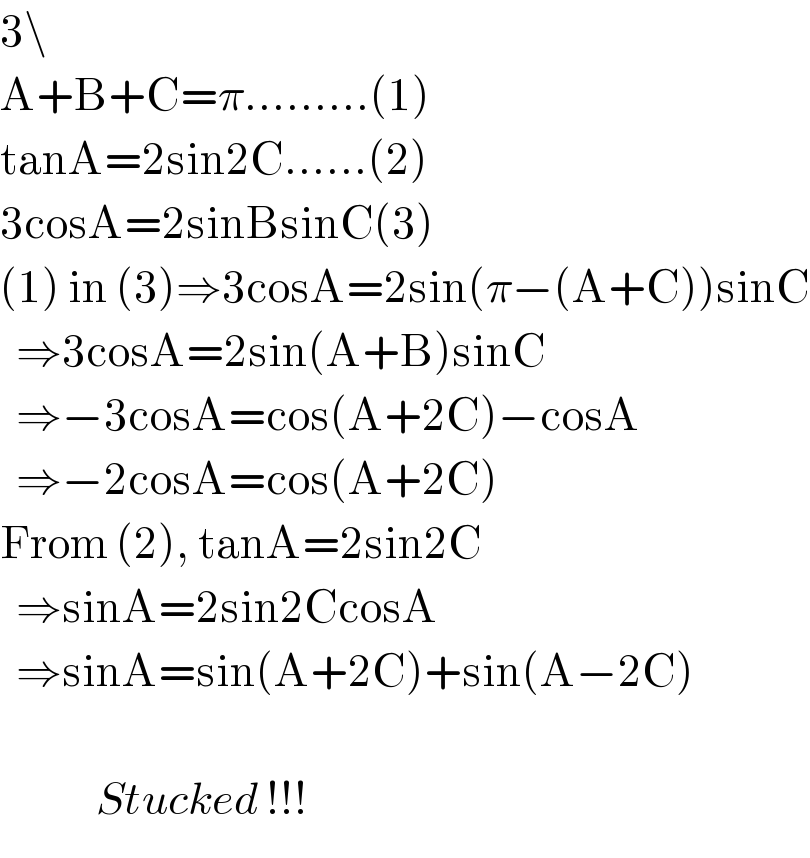
$$\mathrm{3}\backslash \\ $$$$\mathrm{A}+\mathrm{B}+\mathrm{C}=\pi.........\left(\mathrm{1}\right) \\ $$$$\mathrm{tanA}=\mathrm{2sin2C}......\left(\mathrm{2}\right) \\ $$$$\mathrm{3cosA}=\mathrm{2sinBsinC}\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{in}\:\left(\mathrm{3}\right)\Rightarrow\mathrm{3cosA}=\mathrm{2sin}\left(\pi−\left(\mathrm{A}+\mathrm{C}\right)\right)\mathrm{sinC} \\ $$$$\:\:\Rightarrow\mathrm{3cosA}=\mathrm{2sin}\left(\mathrm{A}+\mathrm{B}\right)\mathrm{sinC} \\ $$$$\:\:\Rightarrow−\mathrm{3cosA}=\mathrm{cos}\left(\mathrm{A}+\mathrm{2C}\right)−\mathrm{cosA} \\ $$$$\:\:\Rightarrow−\mathrm{2cosA}=\mathrm{cos}\left(\mathrm{A}+\mathrm{2C}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{2}\right),\:\mathrm{tanA}=\mathrm{2sin2C} \\ $$$$\:\:\Rightarrow\mathrm{sinA}=\mathrm{2sin2CcosA} \\ $$$$\:\:\Rightarrow\mathrm{sinA}=\mathrm{sin}\left(\mathrm{A}+\mathrm{2C}\right)+\mathrm{sin}\left(\mathrm{A}−\mathrm{2C}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{Stucked}\:!!! \\ $$
