
Question Number 105440 by Ar Brandon last updated on 28/Jul/20
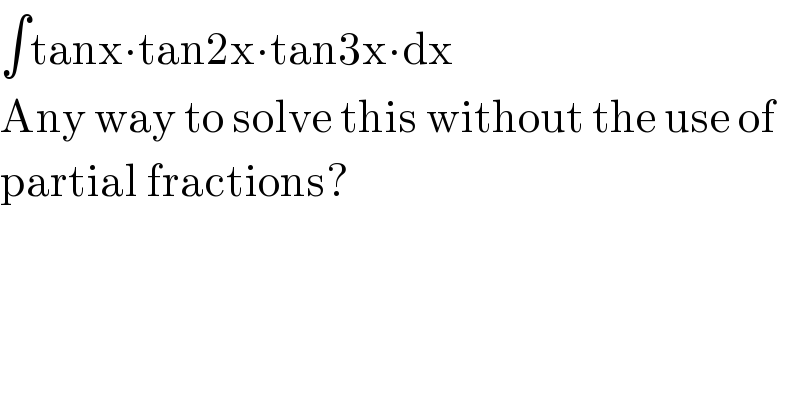
$$\int\mathrm{tanx}\centerdot\mathrm{tan2x}\centerdot\mathrm{tan3x}\centerdot\mathrm{dx} \\ $$$$\mathrm{Any}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{without}\:\mathrm{the}\:\mathrm{use}\:\mathrm{of} \\ $$$$\mathrm{partial}\:\mathrm{fractions}? \\ $$
Commented by som(math1967) last updated on 29/Jul/20
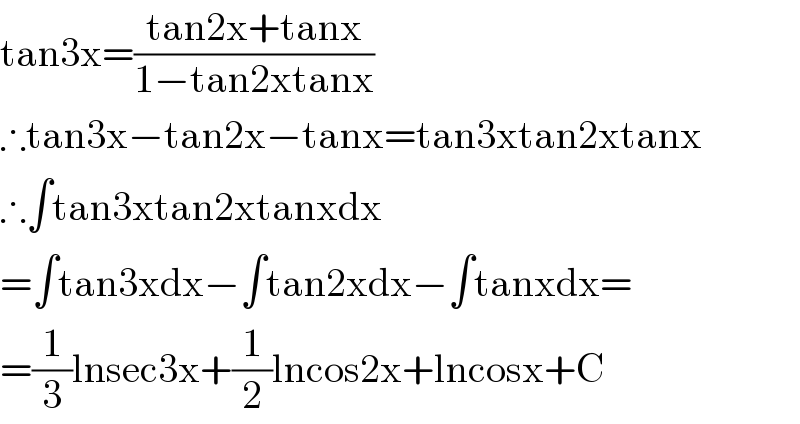
$$\mathrm{tan3x}=\frac{\mathrm{tan2x}+\mathrm{tanx}}{\mathrm{1}−\mathrm{tan2xtanx}} \\ $$$$\therefore\mathrm{tan3x}−\mathrm{tan2x}−\mathrm{tanx}=\mathrm{tan3xtan2xtanx} \\ $$$$\therefore\int\mathrm{tan3xtan2xtanxdx} \\ $$$$=\int\mathrm{tan3xdx}−\int\mathrm{tan2xdx}−\int\mathrm{tanxdx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lnsec3x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lncos2x}+\mathrm{lncosx}+\mathrm{C} \\ $$
Commented by Ar Brandon last updated on 29/Jul/20
$$\mathrm{Wow}!\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}.\:\mathrm{You}\:\mathrm{understood}\:\mathrm{me} \\ $$$$\mathrm{perfectly}. \\ $$
Commented by som(math1967) last updated on 29/Jul/20

$$\mathrm{welcome} \\ $$
Answered by Ar Brandon last updated on 28/Jul/20

$$\mathcal{I}=\int\mathrm{tanx}\centerdot\mathrm{tan2x}\centerdot\mathrm{tan3x}\centerdot\mathrm{dx} \\ $$$$\:\:\:=\int\mathrm{tanx}\centerdot\frac{\mathrm{2tanx}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\centerdot\mathrm{tan3x}\centerdot\mathrm{dx} \\ $$$$\:\:\:=\mathrm{2}\int\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\centerdot\mathrm{tan3x}\centerdot\mathrm{dx}=−\mathrm{2}\int\frac{\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)−\mathrm{1}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\centerdot\mathrm{tan3x}\centerdot\mathrm{dx} \\ $$$$\:\:\:=−\mathrm{2}\int\left\{\mathrm{tan3x}−\frac{\mathrm{tan3x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\right\}\mathrm{dx}=\frac{\mathrm{2ln}\mid\mathrm{cos3x}\mid}{\mathrm{3}}+\mathrm{2}\int\frac{\mathrm{tan3x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{tan3x}=\frac{\mathrm{tan2x}+\mathrm{tanx}}{\mathrm{1}−\mathrm{tan2x}\centerdot\mathrm{tanx}}=\frac{\frac{\mathrm{2tanx}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}+\mathrm{tanx}}{\mathrm{1}−\frac{\mathrm{2tanx}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\mathrm{tanx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2tanx}+\mathrm{tanx}\centerdot\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{2tan}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{3tanx}−\mathrm{tan}^{\mathrm{3}} \mathrm{x}}{\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{tanx}\left(\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{3}\right)}{\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{tanx}\centerdot\left(\left(\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)−\mathrm{8}\right)}{\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\left\{\frac{\mathrm{tanx}\left(\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)}{\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}−\frac{\mathrm{8tanx}}{\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\left\{\mathrm{tanx}−\frac{\mathrm{8tanx}}{\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}\right\} \\ $$$$\Rightarrow\frac{\mathrm{tan3x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{tanx}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{8tanx}}{\left(\mathrm{3tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\left(\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)}\right\} \\ $$$$ \\ $$$$\mathrm{Here}\:\mathrm{is}\:\mathrm{my}\:\mathrm{try}.\:\mathrm{What}\:\mathrm{can}\:\mathrm{be}\:\mathrm{done}\:\mathrm{next}? \\ $$
Commented by malwaan last updated on 29/Jul/20
$${try}\:{to}\:{use}\:{the}\:{short}\:{way}\:{sir} \\ $$
