
Question Number 105290 by bemath last updated on 27/Jul/20

$$\mathcal{G}{iven}\:\frac{\mathrm{sin}\:\mathrm{2}{a}−\mathrm{sin}\:\mathrm{2}{b}}{\mathrm{cos}\:\mathrm{2}{a}+\mathrm{cos}\:\mathrm{2}{b}}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{cos}\:\left({a}−{b}\right)\: \\ $$
Answered by bobhans last updated on 27/Jul/20
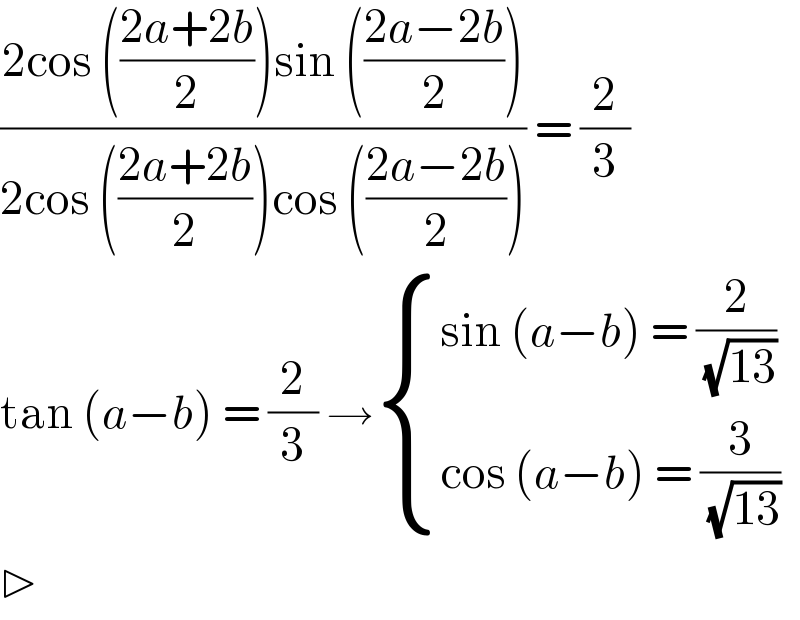
$$\frac{\mathrm{2cos}\:\left(\frac{\mathrm{2}{a}+\mathrm{2}{b}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\mathrm{2}{a}−\mathrm{2}{b}}{\mathrm{2}}\right)}{\mathrm{2cos}\:\left(\frac{\mathrm{2}{a}+\mathrm{2}{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{2}{a}−\mathrm{2}{b}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\left({a}−{b}\right)\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\rightarrow\begin{cases}{\mathrm{sin}\:\left({a}−{b}\right)\:=\:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}}}\\{\mathrm{cos}\:\left({a}−{b}\right)\:=\:\frac{\mathrm{3}}{\sqrt{\mathrm{13}}}}\end{cases} \\ $$$$\triangleright \\ $$
Commented by malwaan last updated on 27/Jul/20

$${tan}\left({a}−{b}\right)\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{{sin}\left({a}−{b}\right)}{{cos}\left({a}−{b}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${cos}\left({a}−{b}\right)\:=\frac{\mathrm{3}}{\mathrm{2}}{sin}\left({a}−{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \left({a}−{b}\right)} \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{9}}{cos}^{\mathrm{2}} \left({a}−{b}\right)=\mathrm{1}−{cos}^{\mathrm{2}} \left({a}−{b}\right) \\ $$$$\Rightarrow\frac{\mathrm{13}}{\mathrm{9}}{cos}^{\mathrm{2}} \left({a}−{b}\right)=\mathrm{1} \\ $$$$\Rightarrow\:{cos}\left({a}−{b}\right)=\:\pm\:\frac{\mathrm{3}}{\sqrt{\mathrm{13}}} \\ $$$$;{sin}\left({a}−{b}\right)=\:\frac{\mathrm{2}}{\mathrm{3}}\:{cos}\left({a}−{b}\right) \\ $$$$\:\:\:\:\:\:\:=\:\pm\:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Jul/20
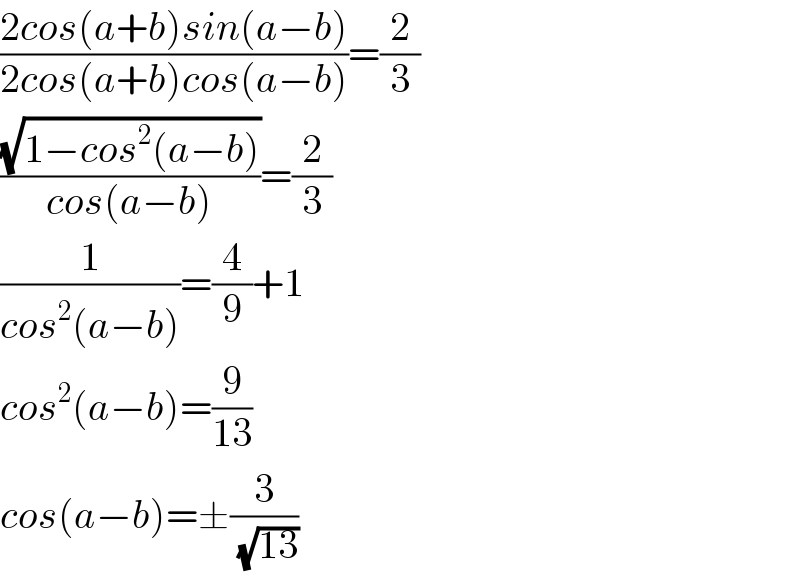
$$\frac{\mathrm{2}{cos}\left({a}+{b}\right){sin}\left({a}−{b}\right)}{\mathrm{2}{cos}\left({a}+{b}\right){cos}\left({a}−{b}\right)}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \left({a}−{b}\right)}}{{cos}\left({a}−{b}\right)}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({a}−{b}\right)}=\frac{\mathrm{4}}{\mathrm{9}}+\mathrm{1} \\ $$$${cos}^{\mathrm{2}} \left({a}−{b}\right)=\frac{\mathrm{9}}{\mathrm{13}} \\ $$$${cos}\left({a}−{b}\right)=\pm\frac{\mathrm{3}}{\sqrt{\mathrm{13}}} \\ $$
