
Question Number 105130 by 175mohamed last updated on 26/Jul/20
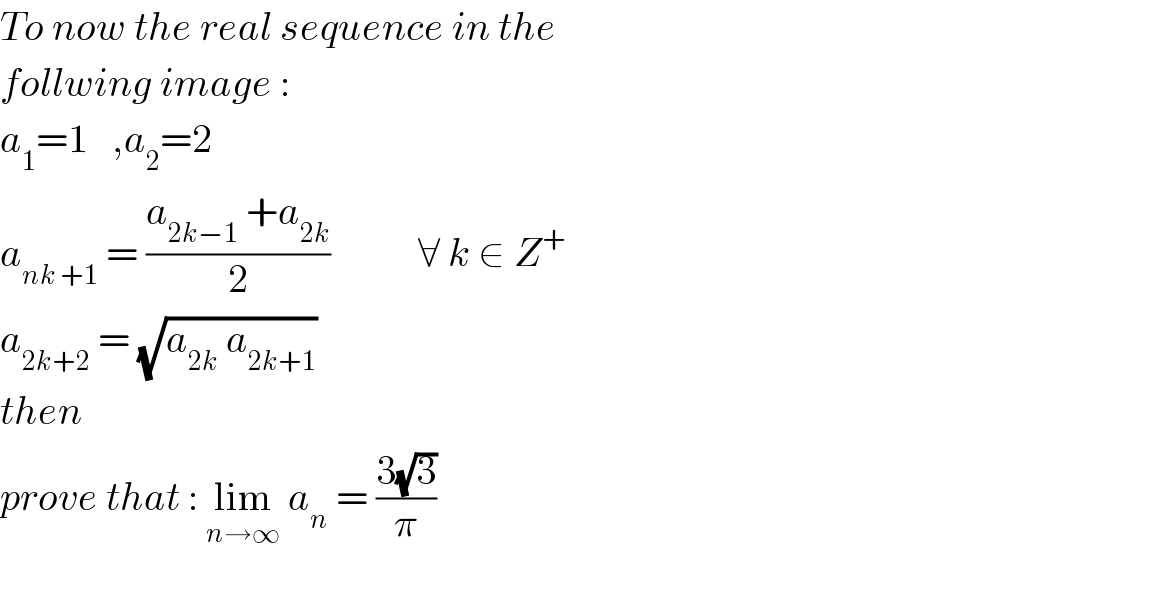
$${To}\:{now}\:{the}\:{real}\:{sequence}\:{in}\:{the} \\ $$$${follwing}\:{image}\:: \\ $$$${a}_{\mathrm{1}} =\mathrm{1}\:\:\:,{a}_{\mathrm{2}} =\mathrm{2} \\ $$$${a}_{{nk}\:+\mathrm{1}} \:=\:\frac{{a}_{\mathrm{2}{k}−\mathrm{1}} \:+{a}_{\mathrm{2}{k}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\forall\:{k}\:\in\:{Z}^{+} \\ $$$${a}_{\mathrm{2}{k}+\mathrm{2}} \:=\:\sqrt{{a}_{\mathrm{2}{k}} \:{a}_{\mathrm{2}{k}+\mathrm{1}} } \\ $$$${then}\: \\ $$$${prove}\:{that}\::\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\pi} \\ $$$$ \\ $$
