
Question Number 104980 by I want to learn more last updated on 25/Jul/20
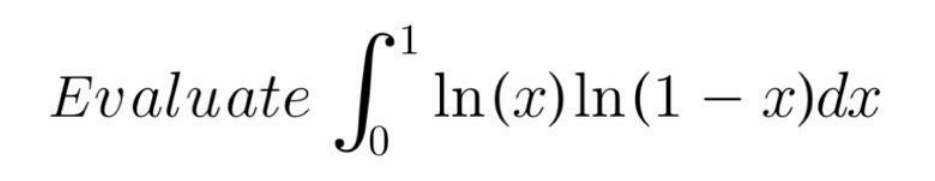
Commented by Dwaipayan Shikari last updated on 25/Jul/20

Commented by I want to learn more last updated on 25/Jul/20
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jul/20
https://youtu.be/q9jbmEGClSk watch this video ��
Answered by profdepo last updated on 25/Jul/20
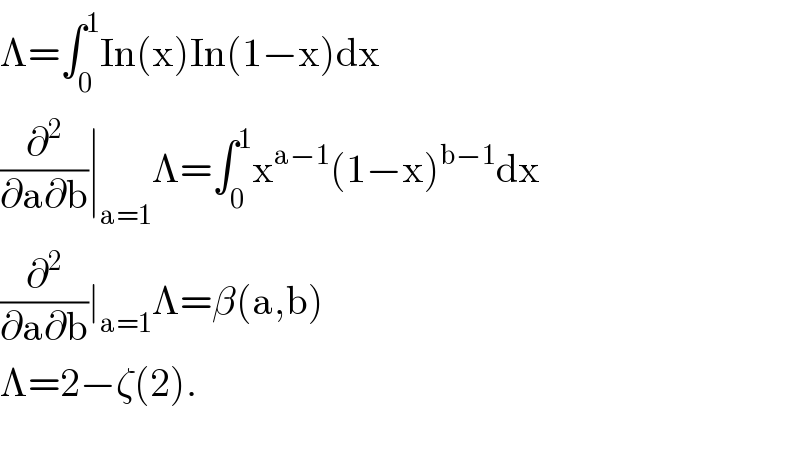
$$\Lambda=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{In}\left(\mathrm{x}\right)\mathrm{In}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\frac{\partial^{\mathrm{2}} }{\partial\mathrm{a}\partial\mathrm{b}}\mid_{\mathrm{a}=\mathrm{1}} \Lambda=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{a}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{b}−\mathrm{1}} \mathrm{dx} \\ $$$$\frac{\partial^{\mathrm{2}} }{\partial\mathrm{a}\partial\mathrm{b}}\mid_{\mathrm{a}=\mathrm{1}} \Lambda=\beta\left(\mathrm{a},\mathrm{b}\right) \\ $$$$\Lambda=\mathrm{2}−\zeta\left(\mathrm{2}\right). \\ $$$$ \\ $$
Commented by I want to learn more last updated on 25/Jul/20
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
