
Question Number 104796 by mathocean1 last updated on 23/Jul/20
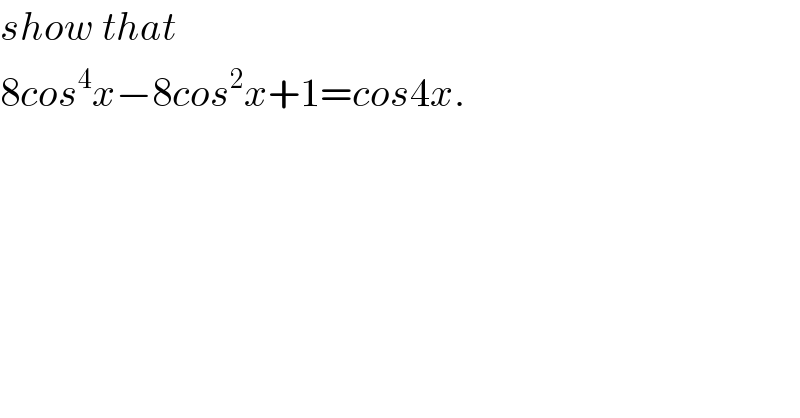
$${show}\:{that}\: \\ $$$$\mathrm{8}{cos}^{\mathrm{4}} {x}−\mathrm{8}{cos}^{\mathrm{2}} {x}+\mathrm{1}={cos}\mathrm{4}{x}. \\ $$
Commented by kaivan.ahmadi last updated on 23/Jul/20
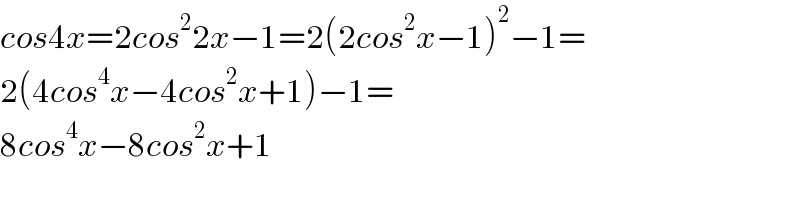
$${cos}\mathrm{4}{x}=\mathrm{2}{cos}^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}=\mathrm{2}\left(\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}= \\ $$$$\mathrm{2}\left(\mathrm{4}{cos}^{\mathrm{4}} {x}−\mathrm{4}{cos}^{\mathrm{2}} {x}+\mathrm{1}\right)−\mathrm{1}= \\ $$$$\mathrm{8}{cos}^{\mathrm{4}} {x}−\mathrm{8}{cos}^{\mathrm{2}} {x}+\mathrm{1} \\ $$
Commented by mathocean1 last updated on 23/Jul/20

$${thank}\:{you}\:{sir}. \\ $$
Answered by a.lgnaoui last updated on 24/Jul/20
![8cos^4 x−8cos^2 x+1=2(2cos^2 x−1)^2 −1=2[cos^2 (2x)]−1=cos 4x](Q104815.png)
$$\mathrm{8cos}\:^{\mathrm{4}} {x}−\mathrm{8cos}\:^{\mathrm{2}} {x}+\mathrm{1}=\mathrm{2}\left(\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{2}\left[\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}{x}\right)\right]−\mathrm{1}=\mathrm{cos}\:\mathrm{4}{x} \\ $$$$ \\ $$
