
Question Number 103998 by M±th+et+s last updated on 18/Jul/20
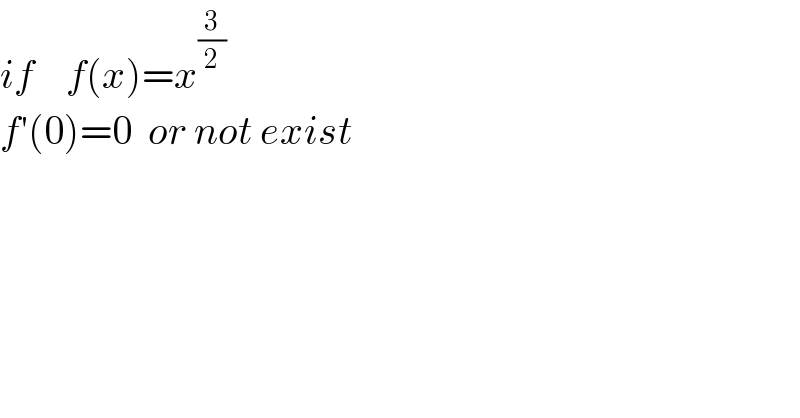
$${if}\:\:\:\:{f}\left({x}\right)={x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${f}'\left(\mathrm{0}\right)=\mathrm{0}\:\:{or}\:{not}\:{exist} \\ $$
Commented by M±th+et+s last updated on 19/Jul/20
Commented by M±th+et+s last updated on 19/Jul/20

Commented by M±th+et+s last updated on 19/Jul/20
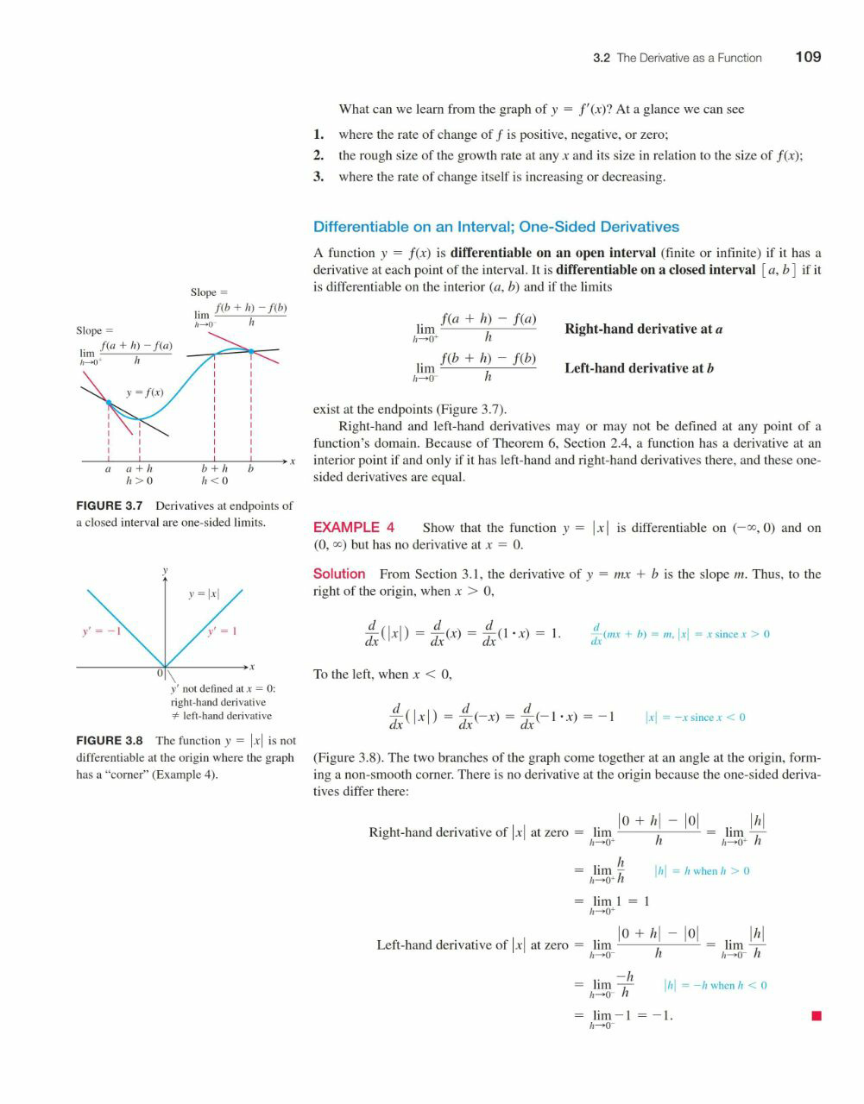
After reviewing some books I found this
Commented by M±th+et+s last updated on 19/Jul/20
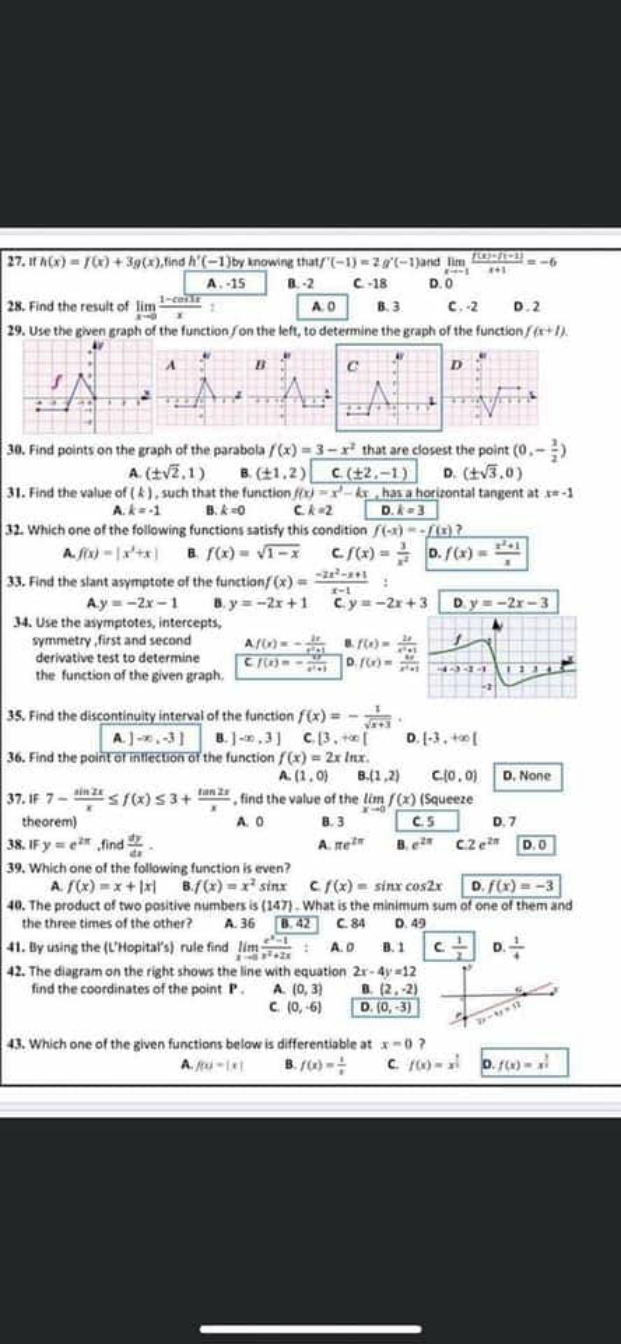
Commented by M±th+et+s last updated on 19/Jul/20
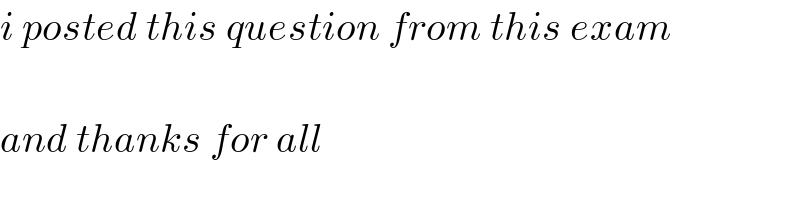
$${i}\:{posted}\:{this}\:{question}\:{from}\:{this}\:{exam}\: \\ $$$$ \\ $$$${and}\:{thanks}\:{for}\:{all} \\ $$
Answered by frc2crc last updated on 18/Jul/20
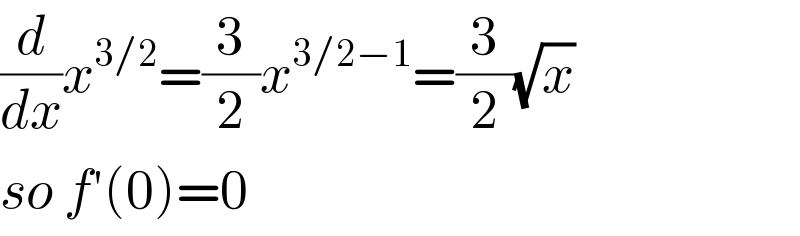
$$\frac{{d}}{{dx}}{x}^{\mathrm{3}/\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{3}/\mathrm{2}−\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}} \\ $$$${so}\:{f}'\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Commented by M±th+et+s last updated on 18/Jul/20
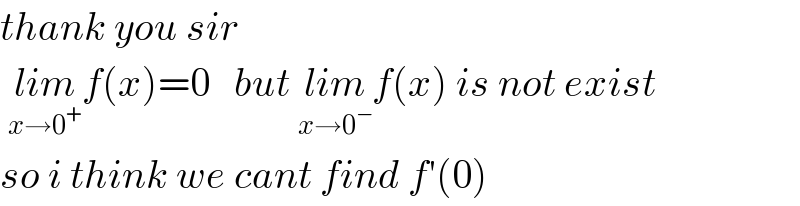
$${thank}\:{you}\:{sir}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}f}\left({x}\right)=\mathrm{0}\:\:\:{but}\:\underset{{x}\rightarrow\mathrm{0}^{−} } {{lim}f}\left({x}\right)\:{is}\:{not}\:{exist} \\ $$$${so}\:{i}\:{think}\:{we}\:{cant}\:{find}\:{f}'\left(\mathrm{0}\right)\: \\ $$
Commented by frc2crc last updated on 18/Jul/20

$${it}\:{doesn}'{t}\:{make}\:{any}\:{sense} \\ $$$$\sqrt{{x}\:}{is}\:'{only}'\:{for}\:{positive} \\ $$$${numbers},{why}\:{do}\:{you}\:{need} \\ $$$${a}\:{limit}? \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 18/Jul/20
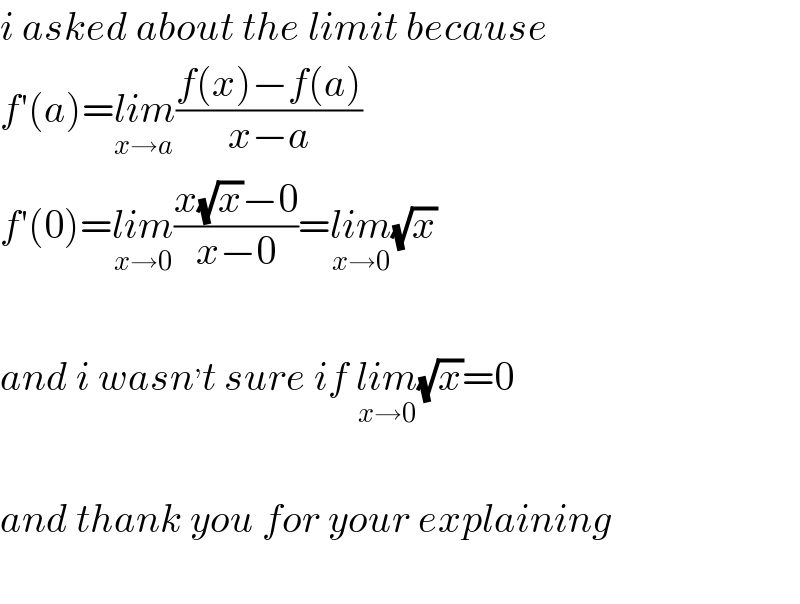
$${i}\:{asked}\:{about}\:{the}\:{limit}\:{because} \\ $$$${f}'\left({a}\right)=\underset{{x}\rightarrow{a}} {{lim}}\frac{{f}\left({x}\right)−{f}\left({a}\right)}{{x}−{a}} \\ $$$${f}'\left(\mathrm{0}\right)=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{x}\sqrt{{x}}−\mathrm{0}}{{x}−\mathrm{0}}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\sqrt{{x}} \\ $$$$ \\ $$$${and}\:{i}\:{wasn}^{,} {t}\:{sure}\:{if}\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\sqrt{{x}}=\mathrm{0} \\ $$$$ \\ $$$${and}\:{thank}\:{you}\:{for}\:{your}\:{explaining} \\ $$$$ \\ $$
Answered by OlafThorendsen last updated on 18/Jul/20
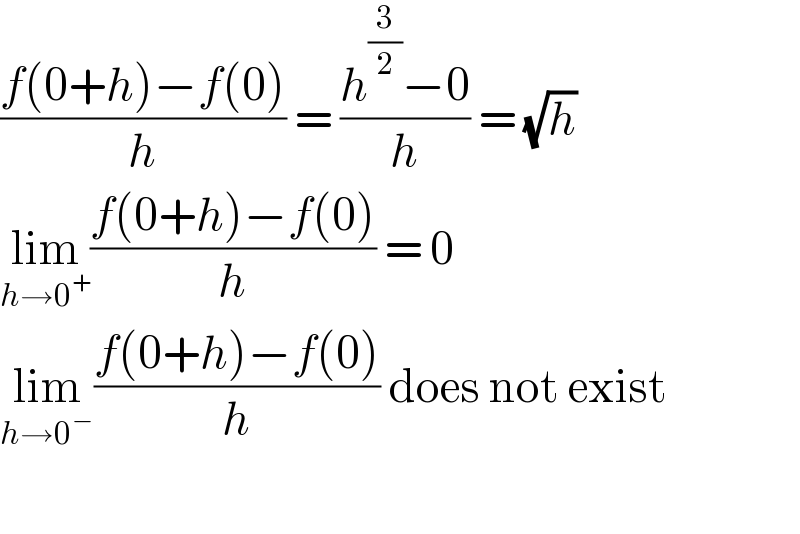
$$\frac{{f}\left(\mathrm{0}+{h}\right)−{f}\left(\mathrm{0}\right)}{{h}}\:=\:\frac{{h}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{0}}{{h}}\:=\:\sqrt{{h}} \\ $$$$\underset{{h}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{f}\left(\mathrm{0}+{h}\right)−{f}\left(\mathrm{0}\right)}{{h}}\:=\:\mathrm{0} \\ $$$$\underset{{h}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{{f}\left(\mathrm{0}+{h}\right)−{f}\left(\mathrm{0}\right)}{{h}}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist} \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 18/Jul/20
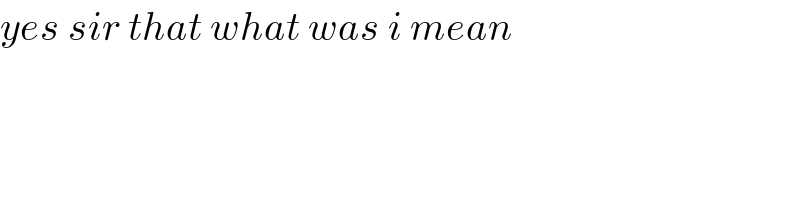
$${yes}\:{sir}\:{that}\:{what}\:{was}\:{i}\:{mean} \\ $$
Commented by bubugne last updated on 18/Jul/20
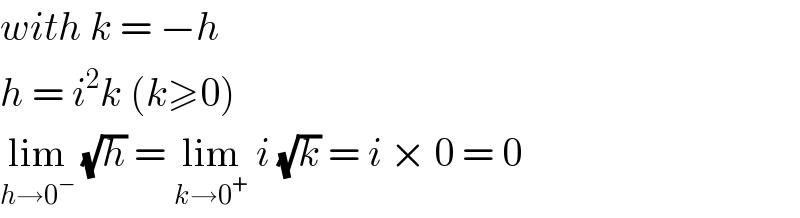
$${with}\:{k}\:=\:−{h} \\ $$$${h}\:=\:{i}^{\mathrm{2}} {k}\:\left({k}\geqslant\mathrm{0}\right) \\ $$$$\underset{{h}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\sqrt{{h}}\:=\:\underset{{k}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{i}\:\sqrt{{k}}\:=\:{i}\:×\:\mathrm{0}\:=\:\mathrm{0} \\ $$
Commented by prakash jain last updated on 18/Jul/20

$$\mathrm{If}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{has} \\ $$$$\mathrm{left}\:\mathrm{end}\:\mathrm{point}\:\mathrm{then}\:\mathrm{you}\:\mathrm{only}\:\mathrm{need} \\ $$$$\mathrm{RHL}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{continuity}.\:\mathrm{You} \\ $$$$\mathrm{do}\:\mathrm{not}\:\mathrm{go}\:\mathrm{outside}\:\mathrm{of}\:\mathrm{domain}\:\mathrm{and} \\ $$$$\mathrm{say}\:\mathrm{function}\:\mathrm{is}\:\mathrm{discontinuous}. \\ $$$${f}\left({x}\right)=\sqrt{{x}}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{at}\:{x}=\mathrm{0}. \\ $$
Answered by Ar Brandon last updated on 18/Jul/20
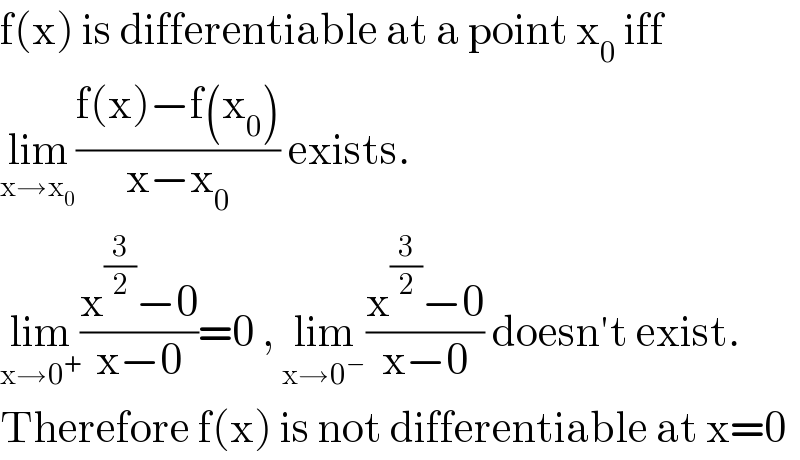
$$\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{differentiable}\:\mathrm{at}\:\mathrm{a}\:\mathrm{point}\:\mathrm{x}_{\mathrm{0}} \:\mathrm{iff} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{x}_{\mathrm{0}} } {\mathrm{lim}}\frac{\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{x}_{\mathrm{0}} \right)}{\mathrm{x}−\mathrm{x}_{\mathrm{0}} }\:\mathrm{exists}. \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{0}}{\mathrm{x}−\mathrm{0}}=\mathrm{0}\:,\:\underset{\mathrm{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{0}}{\mathrm{x}−\mathrm{0}}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}. \\ $$$$\mathrm{Therefore}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{differentiable}\:\mathrm{at}\:\mathrm{x}=\mathrm{0} \\ $$
Commented by prakash jain last updated on 18/Jul/20

$$ \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{has} \\ $$$$\mathrm{left}\:\mathrm{end}\:\mathrm{point}\:\mathrm{then}\:\mathrm{you}\:\mathrm{only}\:\mathrm{need} \\ $$$$\mathrm{RHL}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{continuity}.\:\mathrm{You} \\ $$$$\mathrm{do}\:\mathrm{not}\:\mathrm{go}\:\mathrm{outside}\:\mathrm{of}\:\mathrm{domain}\:\mathrm{and} \\ $$$$\mathrm{say}\:\mathrm{function}\:\mathrm{is}\:\mathrm{discontinuous}. \\ $$$${f}\left({x}\right)=\sqrt{{x}}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{at}\:{x}=\mathrm{0}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{incorrect}\:\mathrm{to}\:\mathrm{take}\:\mathrm{LHL}\:\mathrm{for} \\ $$$$\mathrm{function}\:\sqrt{{x}} \\ $$
Commented by Ar Brandon last updated on 19/Jul/20
OK Sir. Thanks for the clarification.
