
Question Number 103881 by bemath last updated on 18/Jul/20
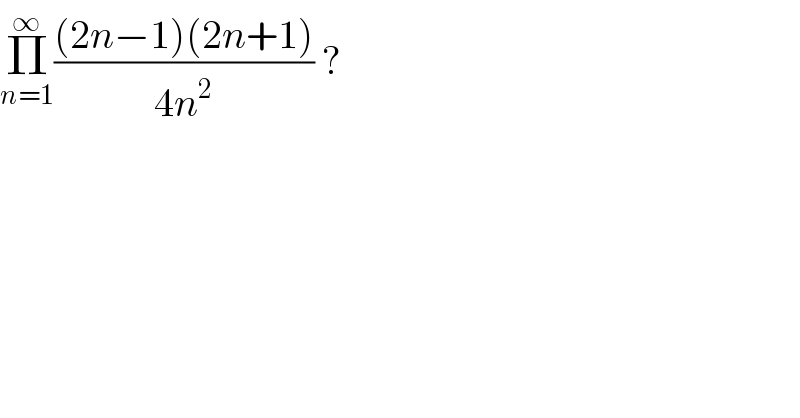
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{4}{n}^{\mathrm{2}} }\:? \\ $$
Answered by bramlex last updated on 18/Jul/20

$${use}\:{Euler}\:{infinity}\:{product}\: \\ $$$$\frac{\mathrm{sin}\:{x}}{{x}}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right) \\ $$$${put}\:{x}\:=\:\frac{\pi}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\right)}{\frac{\pi}{\mathrm{2}}}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{2}}{\pi}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right)\: \\ $$$$\frac{\mathrm{2}}{\pi}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right)=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{4}{n}^{\mathrm{2}} }. \\ $$
Commented by bemath last updated on 18/Jul/20

$${cooll} \\ $$
Answered by mathmax by abdo last updated on 18/Jul/20
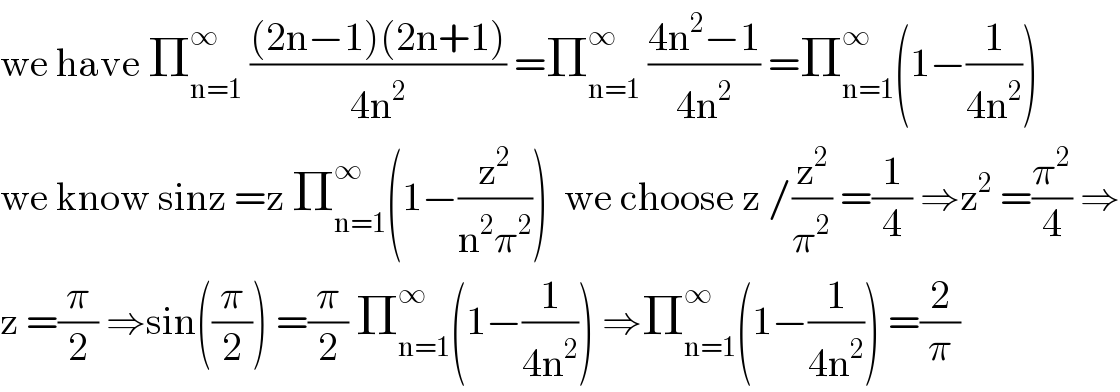
$$\mathrm{we}\:\mathrm{have}\:\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{2n}−\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{4n}^{\mathrm{2}} }\:=\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\:=\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{sinz}\:=\mathrm{z}\:\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right)\:\:\mathrm{we}\:\mathrm{choose}\:\mathrm{z}\:/\frac{\mathrm{z}^{\mathrm{2}} }{\pi^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{z}^{\mathrm{2}} \:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{z}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\right)\:=\frac{\pi}{\mathrm{2}}\:\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\right)\:\Rightarrow\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\right)\:=\frac{\mathrm{2}}{\pi} \\ $$
Commented by bemath last updated on 18/Jul/20

$${thank}\:{you}\:{sir} \\ $$
