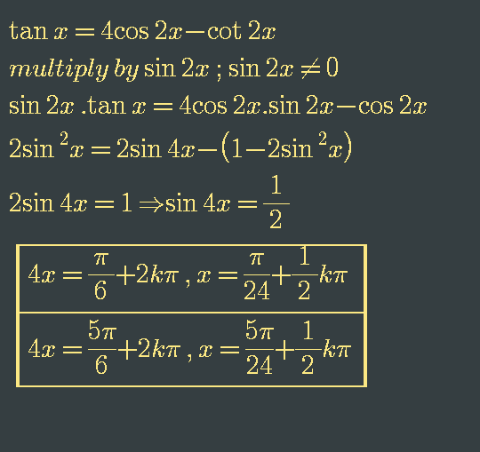Question Number 103823 by bobhans last updated on 17/Jul/20
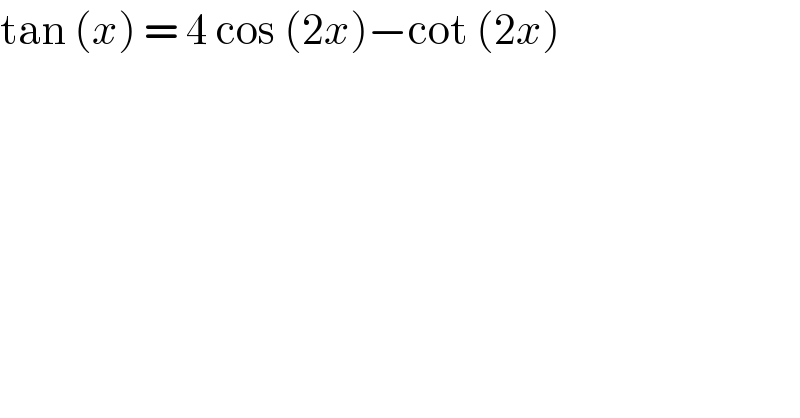
$$\mathrm{tan}\:\left({x}\right)\:=\:\mathrm{4}\:\mathrm{cos}\:\left(\mathrm{2}{x}\right)−\mathrm{cot}\:\left(\mathrm{2}{x}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 17/Jul/20
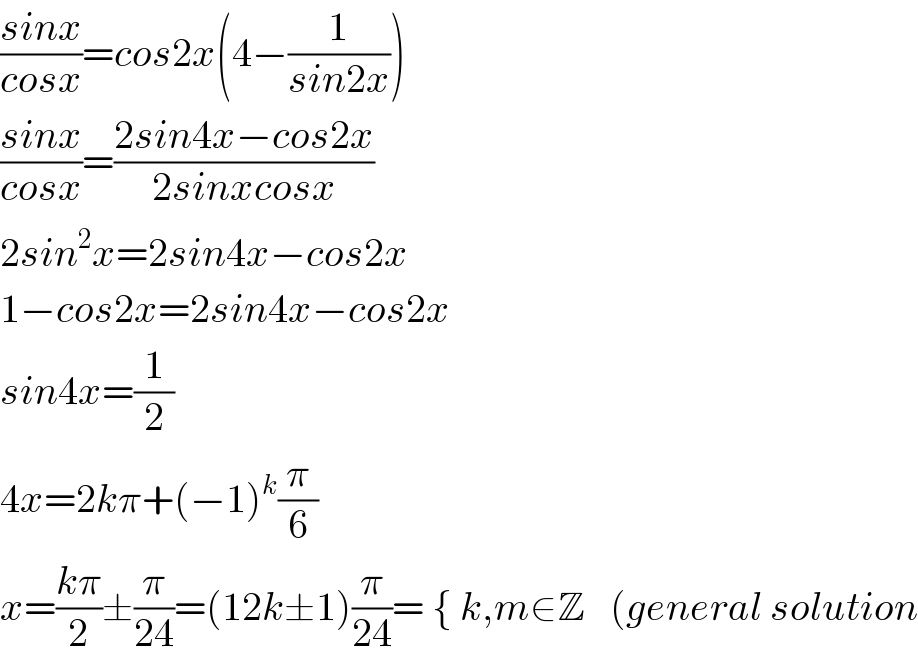
$$\frac{{sinx}}{{cosx}}={cos}\mathrm{2}{x}\left(\mathrm{4}−\frac{\mathrm{1}}{{sin}\mathrm{2}{x}}\right) \\ $$$$\frac{{sinx}}{{cosx}}=\frac{\mathrm{2}{sin}\mathrm{4}{x}−{cos}\mathrm{2}{x}}{\mathrm{2}{sinxcosx}} \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} {x}=\mathrm{2}{sin}\mathrm{4}{x}−{cos}\mathrm{2}{x} \\ $$$$\mathrm{1}−{cos}\mathrm{2}{x}=\mathrm{2}{sin}\mathrm{4}{x}−{cos}\mathrm{2}{x} \\ $$$${sin}\mathrm{4}{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{4}{x}=\mathrm{2}{k}\pi+\left(−\mathrm{1}\right)^{{k}} \frac{\pi}{\mathrm{6}} \\ $$$${x}=\frac{{k}\pi}{\mathrm{2}}\pm\frac{\pi}{\mathrm{24}}=\left(\mathrm{12}{k}\pm\mathrm{1}\right)\frac{\pi}{\mathrm{24}}=\:\left\{\:{k},{m}\in\mathbb{Z}\:\:\:\left({general}\:{solution}\right.\right. \\ $$
Answered by bobhans last updated on 17/Jul/20