
Question Number 103459 by bemath last updated on 15/Jul/20

$${what}\:{are}\:{the}\:{complex}\:{solution}\:\mathrm{tan} \\ $$$$\left({z}\right)\:=\:−\mathrm{2}\:? \\ $$
Commented by mr W last updated on 15/Jul/20

$${z}={k}\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2} \\ $$$${z}\:{is}\:{always}\:{real}! \\ $$
Commented by bemath last updated on 15/Jul/20
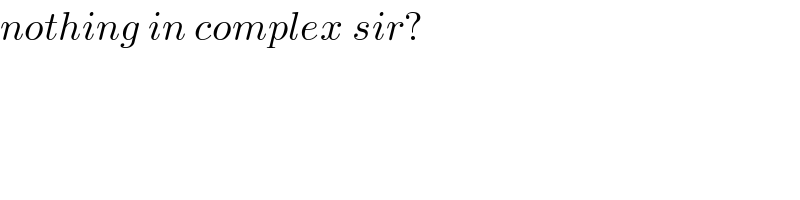
$${nothing}\:{in}\:{complex}\:{sir}? \\ $$
Commented by mr W last updated on 15/Jul/20

$${a}\:{real}\:{number}\:{is}\:{also}\:{a}\:{complex} \\ $$$${number}.\:{if}\:{you}\:{want}, \\ $$$${z}={k}\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{0}{i} \\ $$
Commented by bobhans last updated on 15/Jul/20
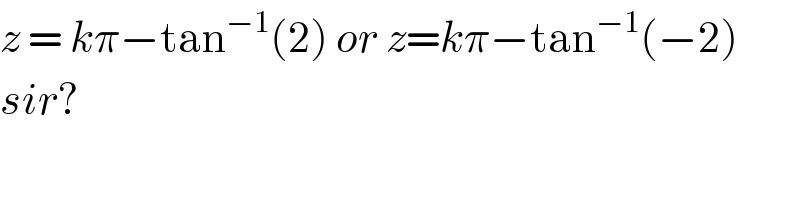
$${z}\:=\:{k}\pi−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\:{or}\:{z}={k}\pi−\mathrm{tan}^{−\mathrm{1}} \left(−\mathrm{2}\right) \\ $$$${sir}? \\ $$
Commented by mr W last updated on 15/Jul/20

$${z}\:=\:{k}\pi−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right) \\ $$
Commented by bramlex last updated on 15/Jul/20
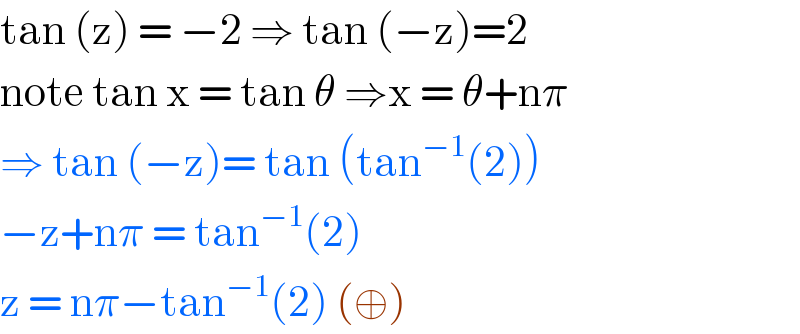
$$\mathrm{tan}\:\left(\mathrm{z}\right)\:=\:−\mathrm{2}\:\Rightarrow\:\mathrm{tan}\:\left(−\mathrm{z}\right)=\mathrm{2} \\ $$$$\mathrm{note}\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{tan}\:\theta\:\Rightarrow\mathrm{x}\:=\:\theta+\mathrm{n}\pi \\ $$$$\Rightarrow\:\mathrm{tan}\:\left(−\mathrm{z}\right)=\:\mathrm{tan}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\right) \\ $$$$−\mathrm{z}+\mathrm{n}\pi\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\: \\ $$$$\mathrm{z}\:=\:\mathrm{n}\pi−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\:\left(\oplus\right) \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
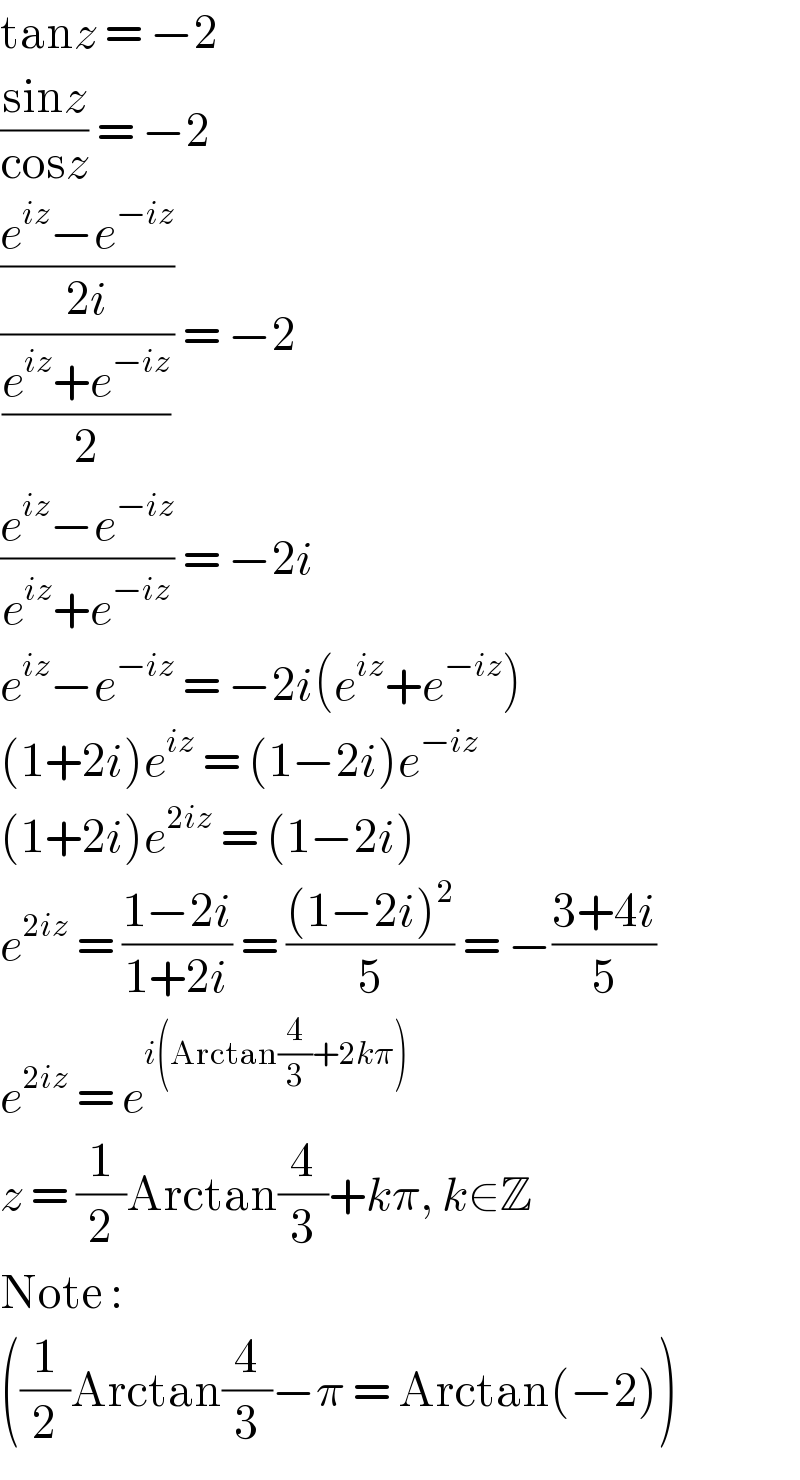
$$\mathrm{tan}{z}\:=\:−\mathrm{2} \\ $$$$\frac{\mathrm{sin}{z}}{\mathrm{cos}{z}}\:=\:−\mathrm{2} \\ $$$$\frac{\frac{{e}^{{iz}} −{e}^{−{iz}} }{\mathrm{2}{i}}}{\frac{{e}^{{iz}} +{e}^{−{iz}} }{\mathrm{2}}}\:=\:−\mathrm{2} \\ $$$$\frac{{e}^{{iz}} −{e}^{−{iz}} }{{e}^{{iz}} +{e}^{−{iz}} }\:=\:−\mathrm{2}{i} \\ $$$${e}^{{iz}} −{e}^{−{iz}} \:=\:−\mathrm{2}{i}\left({e}^{{iz}} +{e}^{−{iz}} \right) \\ $$$$\left(\mathrm{1}+\mathrm{2}{i}\right){e}^{{iz}} \:=\:\left(\mathrm{1}−\mathrm{2}{i}\right){e}^{−{iz}} \\ $$$$\left(\mathrm{1}+\mathrm{2}{i}\right){e}^{\mathrm{2}{iz}} \:=\:\left(\mathrm{1}−\mathrm{2}{i}\right) \\ $$$${e}^{\mathrm{2}{iz}} \:=\:\frac{\mathrm{1}−\mathrm{2}{i}}{\mathrm{1}+\mathrm{2}{i}}\:=\:\frac{\left(\mathrm{1}−\mathrm{2}{i}\right)^{\mathrm{2}} }{\mathrm{5}}\:=\:−\frac{\mathrm{3}+\mathrm{4}{i}}{\mathrm{5}} \\ $$$${e}^{\mathrm{2}{iz}} \:=\:{e}^{{i}\left(\mathrm{Arctan}\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}{k}\pi\right)} \\ $$$${z}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Arctan}\frac{\mathrm{4}}{\mathrm{3}}+{k}\pi,\:{k}\in\mathbb{Z} \\ $$$$\mathrm{Note}\:: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Arctan}\frac{\mathrm{4}}{\mathrm{3}}−\pi\:=\:\mathrm{Arctan}\left(−\mathrm{2}\right)\right) \\ $$
Answered by mathmax by abdo last updated on 15/Jul/20

$$\mathrm{tanz}\:=−\mathrm{2}\:\Rightarrow\frac{\mathrm{sinz}}{\mathrm{cosz}}=−\mathrm{2}\:\Rightarrow\mathrm{sinz}\:=−\mathrm{2cosz}\:\Rightarrow \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{z}\:=\mathrm{4cos}^{\mathrm{2}} \mathrm{z}\:\Rightarrow\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{z}\:=\mathrm{4cos}^{\mathrm{2}} \mathrm{z}\:\Rightarrow\mathrm{1}\:=\mathrm{5cos}^{\mathrm{2}} \mathrm{z}\:\Rightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \mathrm{z}\:=\frac{\mathrm{1}}{\mathrm{5}}\:\Rightarrow\mathrm{cosz}\:=\overset{−} {+}\frac{\mathrm{1}}{\sqrt{\mathrm{5}}} \\ $$$$\mathrm{cosz}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{ch}\left(\mathrm{iz}\right)\:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\Rightarrow\:\frac{\mathrm{e}^{\mathrm{iz}} \:+\mathrm{e}^{−\mathrm{iz}} }{\mathrm{2}}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{e}^{\mathrm{iz}} \:+\mathrm{e}^{−\mathrm{iz}} \:=\frac{\mathrm{2}}{\sqrt{\mathrm{5}}} \\ $$$$\mathrm{e}^{\mathrm{iz}} \:=\mathrm{t}\:\Rightarrow\mathrm{t}+\mathrm{t}^{−\mathrm{1}} \:=\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\mathrm{t}\:\Rightarrow\mathrm{t}^{\mathrm{2}} \:−\frac{\mathrm{2t}}{\sqrt{\mathrm{5}}}\:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow \\ $$$$\sqrt{\mathrm{5}}\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\sqrt{\mathrm{5}}=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{1}−\mathrm{5}\:=−\mathrm{4}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\mathrm{1}+\mathrm{2i}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\mathrm{1}−\mathrm{2i}\: \\ $$$$\mathrm{e}^{\mathrm{iz}} \:=\mathrm{t}\:\Rightarrow\mathrm{iz}\:=\mathrm{lnt}\:\Rightarrow\mathrm{z}\:=−\mathrm{iln}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{z}\:=−\mathrm{iln}\left(\mathrm{1}\overset{−} {+}\mathrm{2i}\right) \\ $$$$\mathrm{case}\:\mathrm{2}\:\:\mathrm{cosz}\:=−\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\Rightarrow\frac{\mathrm{e}^{\mathrm{iz}} \:+\mathrm{e}^{−\mathrm{iz}} }{\mathrm{2}}\:=−\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{iz}} \:+\mathrm{e}^{−\mathrm{iz}} \:\:=\frac{−\mathrm{2}}{\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{t}\:+\mathrm{t}^{−\mathrm{1}\:} \:=−\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\:\:\left(\mathrm{t}\:=\mathrm{e}^{\mathrm{iz}} \right)\:\Rightarrow \\ $$$$\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\:=−\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\mathrm{t}\:\Rightarrow\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{2t}}{\sqrt{\mathrm{5}}}\:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\sqrt{\mathrm{5}}\mathrm{t}^{\mathrm{2}} +\mathrm{2t}\:+\sqrt{\mathrm{5}}=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{1}−\mathrm{5}\:=−\mathrm{4}\:\Rightarrow \\ $$$$\mathrm{t}_{\mathrm{1}} =−\mathrm{1}+\mathrm{2i}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =−\mathrm{1}−\mathrm{2i} \\ $$$$\mathrm{z}\:=−\mathrm{iln}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{z}\:=−\mathrm{iln}\left(−\mathrm{1}\:\overset{−} {+}\mathrm{2i}\right) \\ $$$$ \\ $$
Commented by mr W last updated on 15/Jul/20
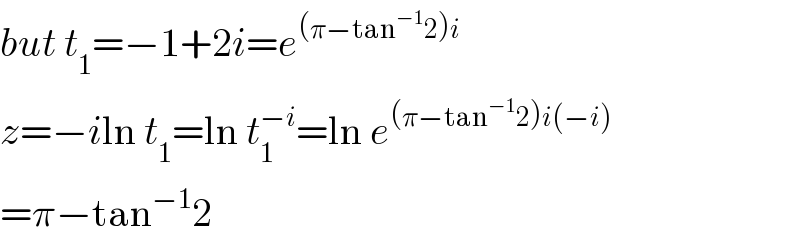
$${but}\:{t}_{\mathrm{1}} =−\mathrm{1}+\mathrm{2}{i}={e}^{\left(\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\right){i}} \\ $$$${z}=−{i}\mathrm{ln}\:{t}_{\mathrm{1}} =\mathrm{ln}\:{t}_{\mathrm{1}} ^{−{i}} =\mathrm{ln}\:{e}^{\left(\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\right){i}\left(−{i}\right)} \\ $$$$=\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 16/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{havent}\:\mathrm{verify}.. \\ $$
