
Previous in Relation and Functions Next in Relation and Functions
Question Number 103457 by bobhans last updated on 15/Jul/20
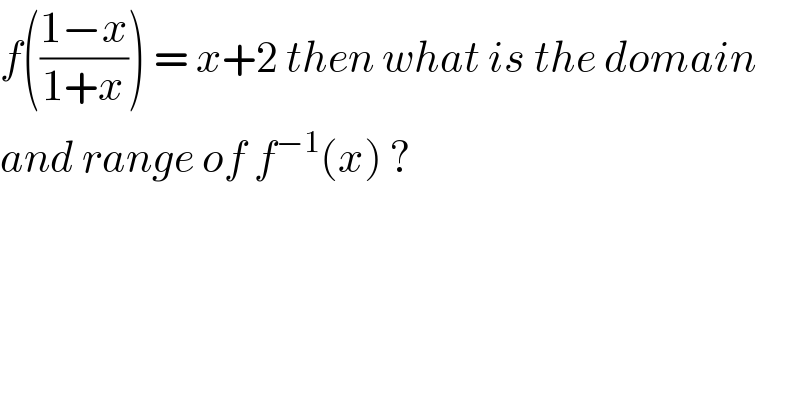
$${f}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)\:=\:{x}+\mathrm{2}\:{then}\:{what}\:{is}\:{the}\:{domain} \\ $$$${and}\:{range}\:{of}\:{f}^{−\mathrm{1}} \left({x}\right)\:? \\ $$
Answered by Worm_Tail last updated on 15/Jul/20
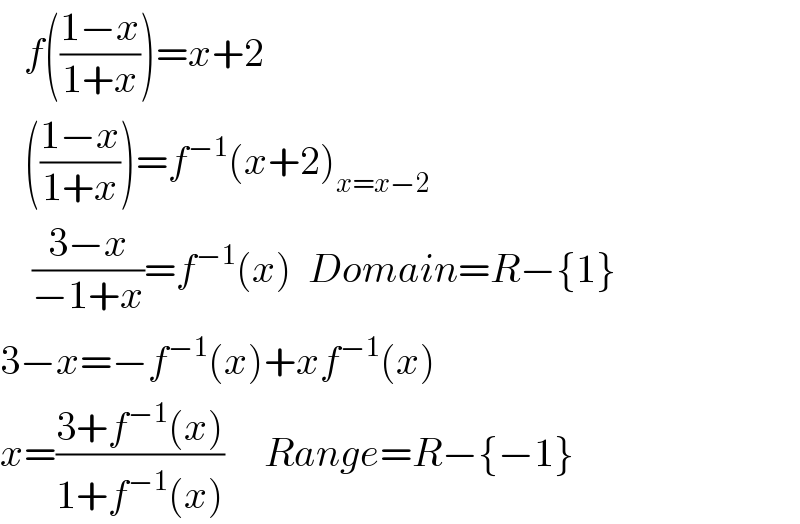
$$\:\:\:{f}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)={x}+\mathrm{2} \\ $$$$\:\:\:\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)={f}^{−\mathrm{1}} \left({x}+\mathrm{2}\right)_{{x}={x}−\mathrm{2}} \\ $$$$\:\:\:\:\frac{\mathrm{3}−{x}}{−\mathrm{1}+{x}}={f}^{−\mathrm{1}} \left({x}\right)\:\:{Domain}={R}−\left\{\mathrm{1}\right\} \\ $$$$\mathrm{3}−{x}=−{f}^{−\mathrm{1}} \left({x}\right)+{xf}^{−\mathrm{1}} \left({x}\right) \\ $$$${x}=\frac{\mathrm{3}+{f}^{−\mathrm{1}} \left({x}\right)}{\mathrm{1}+{f}^{−\mathrm{1}} \left({x}\right)}\:\:\:\:\:{Range}={R}−\left\{−\mathrm{1}\right\} \\ $$
Answered by bemath last updated on 15/Jul/20
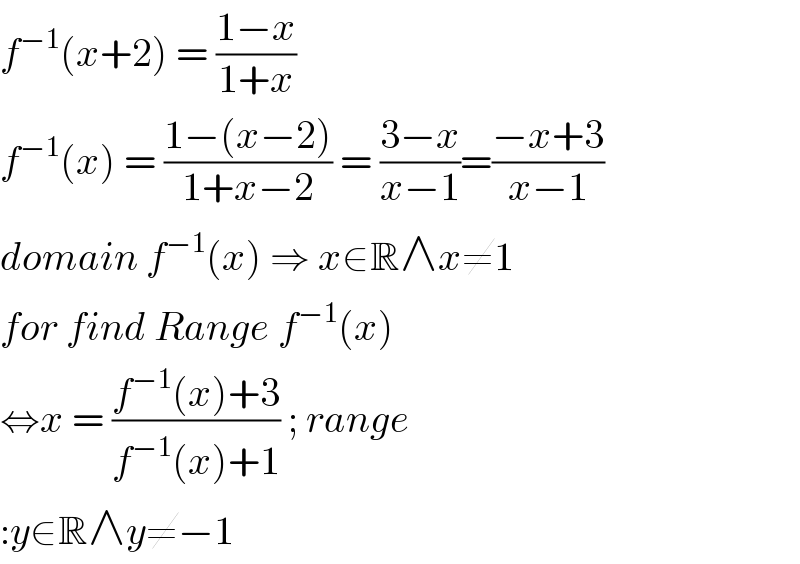
$${f}^{−\mathrm{1}} \left({x}+\mathrm{2}\right)\:=\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{1}−\left({x}−\mathrm{2}\right)}{\mathrm{1}+{x}−\mathrm{2}}\:=\:\frac{\mathrm{3}−{x}}{{x}−\mathrm{1}}=\frac{−{x}+\mathrm{3}}{{x}−\mathrm{1}} \\ $$$${domain}\:{f}^{−\mathrm{1}} \left({x}\right)\:\Rightarrow\:{x}\in\mathbb{R}\wedge{x}\neq\mathrm{1} \\ $$$${for}\:{find}\:{Range}\:{f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\Leftrightarrow{x}\:=\:\frac{{f}^{−\mathrm{1}} \left({x}\right)+\mathrm{3}}{{f}^{−\mathrm{1}} \left({x}\right)+\mathrm{1}}\:;\:{range} \\ $$$$:{y}\in\mathbb{R}\wedge{y}\neq−\mathrm{1} \\ $$
