
Question Number 10318 by Tawakalitu ayo mi last updated on 03/Feb/17

$$\mathrm{If}\:\mathrm{12},\:\mathrm{x},\:\mathrm{y}\:\mathrm{and}\:\mathrm{4}\:\mathrm{provides}\:\mathrm{a}\:\mathrm{sequence}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{3}\:\mathrm{of}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{in}\:\mathrm{arithmetic} \\ $$$$\mathrm{progression}.\:\mathrm{Calculate}\:\mathrm{the}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Possible}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{A}.\mathrm{P} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{The}\:\mathrm{product}\:\mathrm{of}\:\mathrm{the}\:\mathrm{last}\:\mathrm{3}\:\mathrm{numbers}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{G}.\mathrm{P} \\ $$
Answered by mrW1 last updated on 05/Feb/17
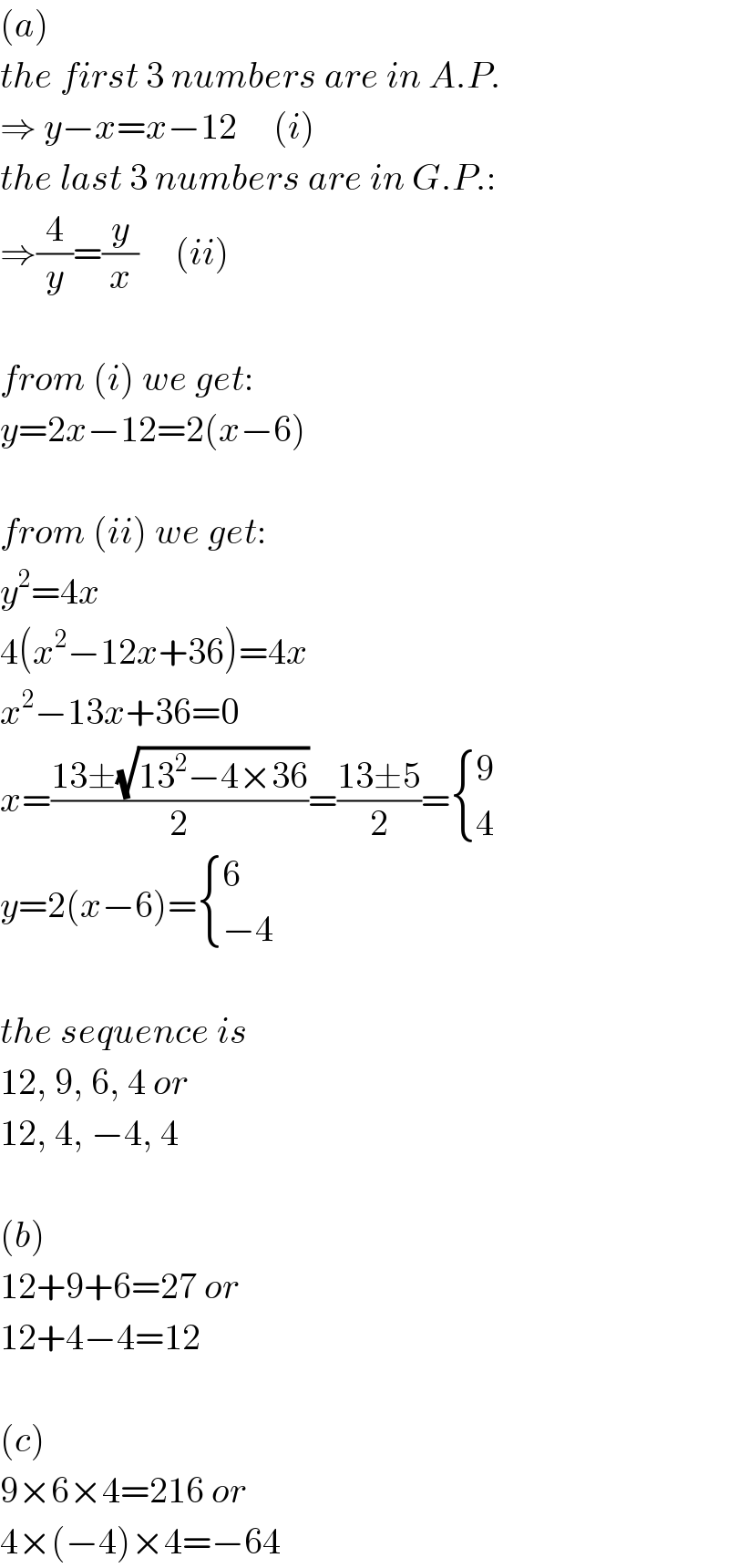
$$\left({a}\right) \\ $$$${the}\:{first}\:\mathrm{3}\:{numbers}\:{are}\:{in}\:{A}.{P}. \\ $$$$\Rightarrow\:{y}−{x}={x}−\mathrm{12}\:\:\:\:\:\left({i}\right) \\ $$$${the}\:{last}\:\mathrm{3}\:{numbers}\:{are}\:{in}\:{G}.{P}.: \\ $$$$\Rightarrow\frac{\mathrm{4}}{{y}}=\frac{{y}}{{x}}\:\:\:\:\:\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{we}\:{get}: \\ $$$${y}=\mathrm{2}{x}−\mathrm{12}=\mathrm{2}\left({x}−\mathrm{6}\right) \\ $$$$ \\ $$$${from}\:\left({ii}\right)\:{we}\:{get}: \\ $$$${y}^{\mathrm{2}} =\mathrm{4}{x} \\ $$$$\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{36}\right)=\mathrm{4}{x} \\ $$$${x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{36}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{13}\pm\sqrt{\mathrm{13}^{\mathrm{2}} −\mathrm{4}×\mathrm{36}}}{\mathrm{2}}=\frac{\mathrm{13}\pm\mathrm{5}}{\mathrm{2}}=\begin{cases}{\mathrm{9}}\\{\mathrm{4}}\end{cases} \\ $$$${y}=\mathrm{2}\left({x}−\mathrm{6}\right)=\begin{cases}{\mathrm{6}}\\{−\mathrm{4}}\end{cases} \\ $$$$ \\ $$$${the}\:{sequence}\:{is} \\ $$$$\mathrm{12},\:\mathrm{9},\:\mathrm{6},\:\mathrm{4}\:{or} \\ $$$$\mathrm{12},\:\mathrm{4},\:−\mathrm{4},\:\mathrm{4} \\ $$$$ \\ $$$$\left({b}\right) \\ $$$$\mathrm{12}+\mathrm{9}+\mathrm{6}=\mathrm{27}\:{or} \\ $$$$\mathrm{12}+\mathrm{4}−\mathrm{4}=\mathrm{12} \\ $$$$ \\ $$$$\left({c}\right) \\ $$$$\mathrm{9}×\mathrm{6}×\mathrm{4}=\mathrm{216}\:{or} \\ $$$$\mathrm{4}×\left(−\mathrm{4}\right)×\mathrm{4}=−\mathrm{64} \\ $$
Commented by Tawakalitu ayo mi last updated on 04/Feb/17

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless} \\ $$$$\mathrm{you}\:\mathrm{sir}. \\ $$
