
Question Number 102769 by ajfour last updated on 11/Jul/20
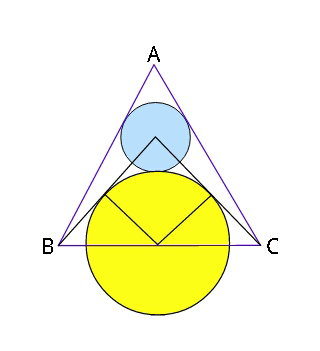
Commented by bramlex last updated on 11/Jul/20
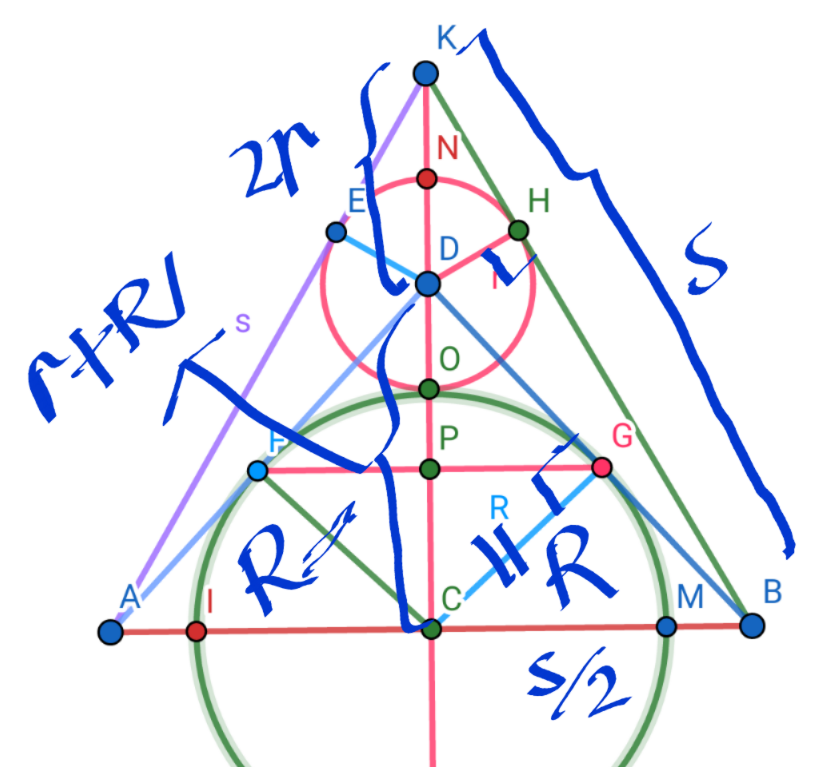
Commented by bramlex last updated on 11/Jul/20
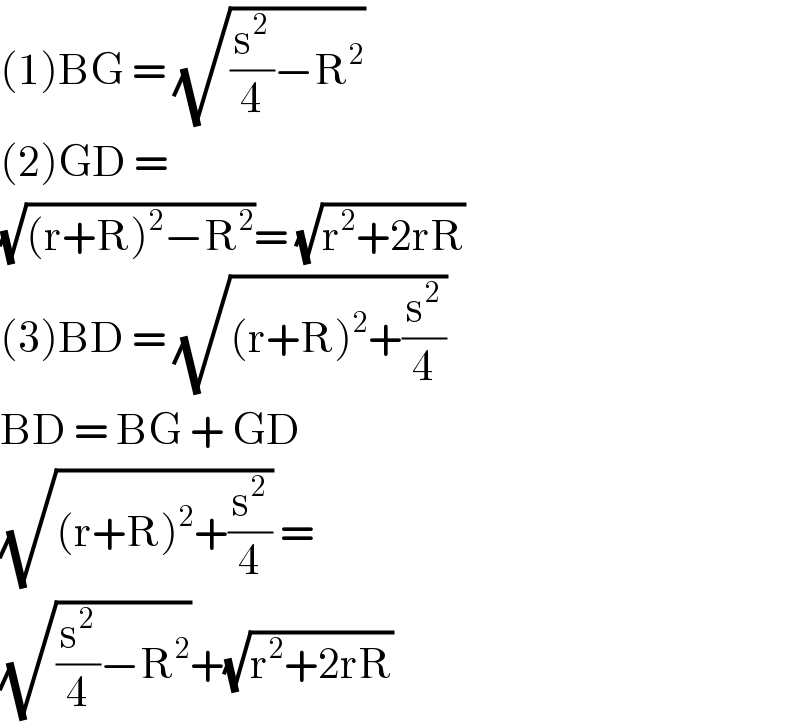
$$\left(\mathrm{1}\right)\mathrm{BG}\:=\:\sqrt{\frac{\mathrm{s}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{R}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\mathrm{GD}\:= \\ $$$$\sqrt{\left(\mathrm{r}+\mathrm{R}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} }=\:\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{2rR}} \\ $$$$\left(\mathrm{3}\right)\mathrm{BD}\:=\:\sqrt{\left(\mathrm{r}+\mathrm{R}\right)^{\mathrm{2}} +\frac{\mathrm{s}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\mathrm{BD}\:=\:\mathrm{BG}\:+\:\mathrm{GD} \\ $$$$\sqrt{\left(\mathrm{r}+\mathrm{R}\right)^{\mathrm{2}} +\frac{\mathrm{s}^{\mathrm{2}} }{\mathrm{4}}}\:= \\ $$$$\sqrt{\frac{\mathrm{s}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{R}^{\mathrm{2}} }+\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{2rR}}\: \\ $$
Commented by ajfour last updated on 11/Jul/20
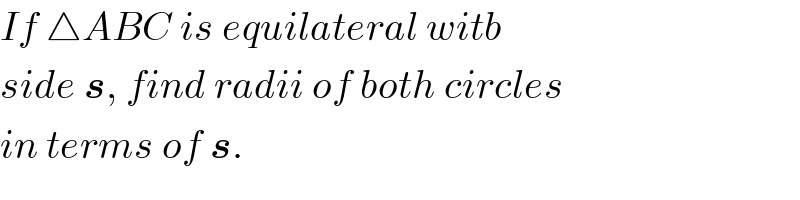
$${If}\:\bigtriangleup{ABC}\:{is}\:{equilateral}\:{witb} \\ $$$${side}\:\boldsymbol{{s}},\:{find}\:{radii}\:{of}\:{both}\:{circles} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{s}}. \\ $$
Commented by bramlex last updated on 11/Jul/20
Commented by bramlex last updated on 11/Jul/20
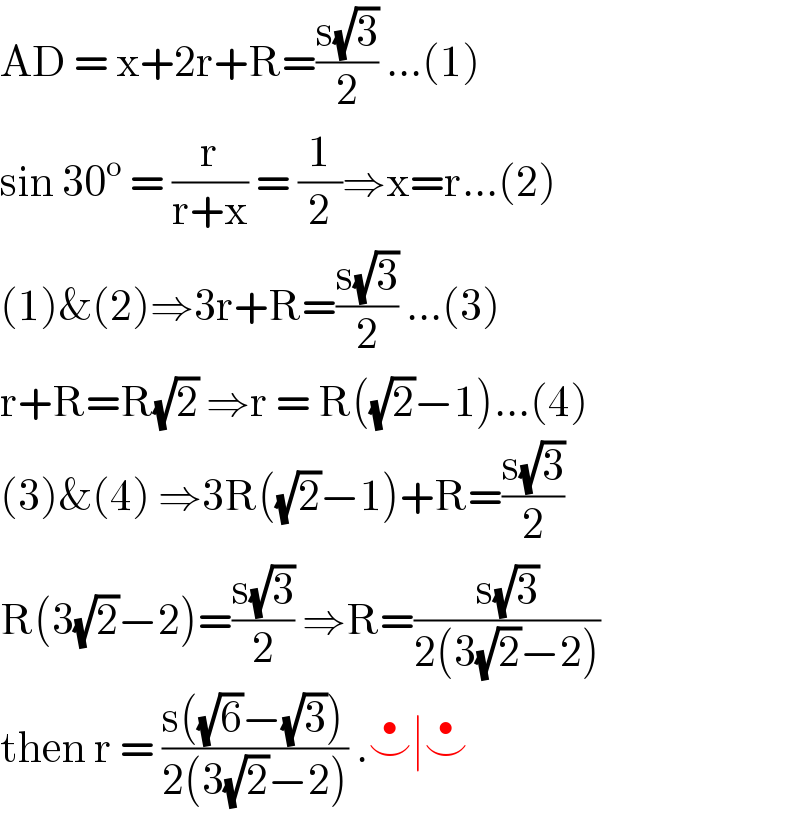
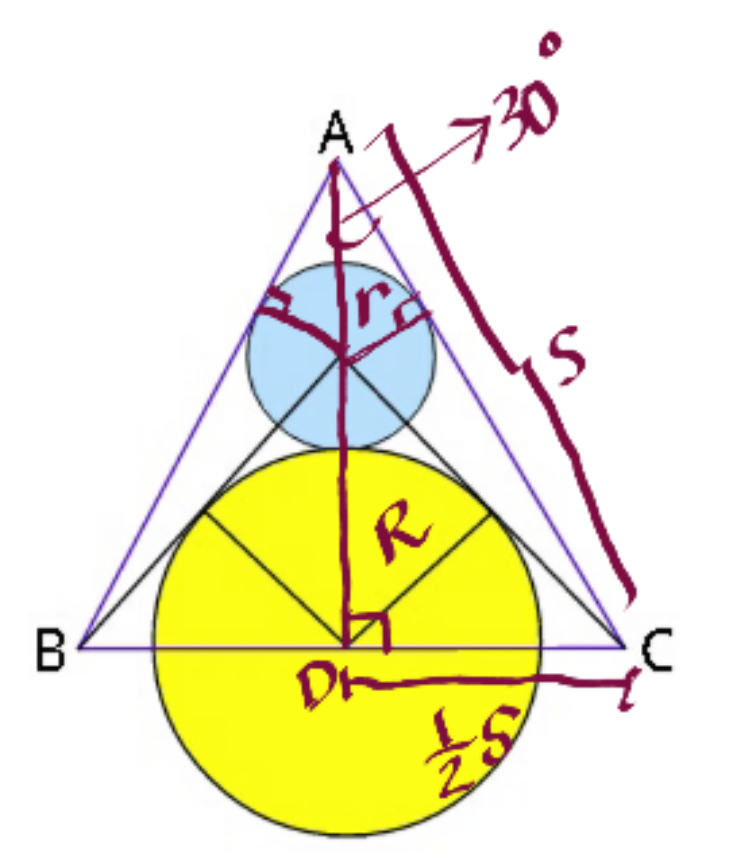
$$\mathrm{AD}\:=\:\mathrm{x}+\mathrm{2r}+\mathrm{R}=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\:...\left(\mathrm{1}\right) \\ $$$$\mathrm{sin}\:\mathrm{30}^{\mathrm{o}} \:=\:\frac{\mathrm{r}}{\mathrm{r}+\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{x}=\mathrm{r}...\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\&\left(\mathrm{2}\right)\Rightarrow\mathrm{3r}+\mathrm{R}=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\:...\left(\mathrm{3}\right) \\ $$$$\mathrm{r}+\mathrm{R}=\mathrm{R}\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{r}\:=\:\mathrm{R}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)...\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{3}\right)\&\left(\mathrm{4}\right)\:\Rightarrow\mathrm{3R}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\mathrm{R}=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{R}\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\right)=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\mathrm{R}=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\right)} \\ $$$$\mathrm{then}\:\mathrm{r}\:=\:\frac{\mathrm{s}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}\right)}{\mathrm{2}\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\right)}\:.\overset{\bullet} {\smile}\mid\overset{\bullet} {\smile}\: \\ $$
Commented by ajfour last updated on 11/Jul/20
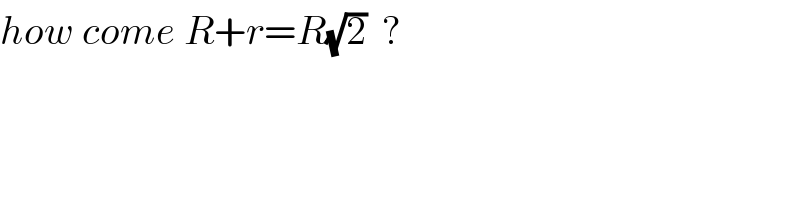
$${how}\:{come}\:{R}+{r}={R}\sqrt{\mathrm{2}}\:\:? \\ $$
Commented by bramlex last updated on 11/Jul/20
Commented by ajfour last updated on 11/Jul/20

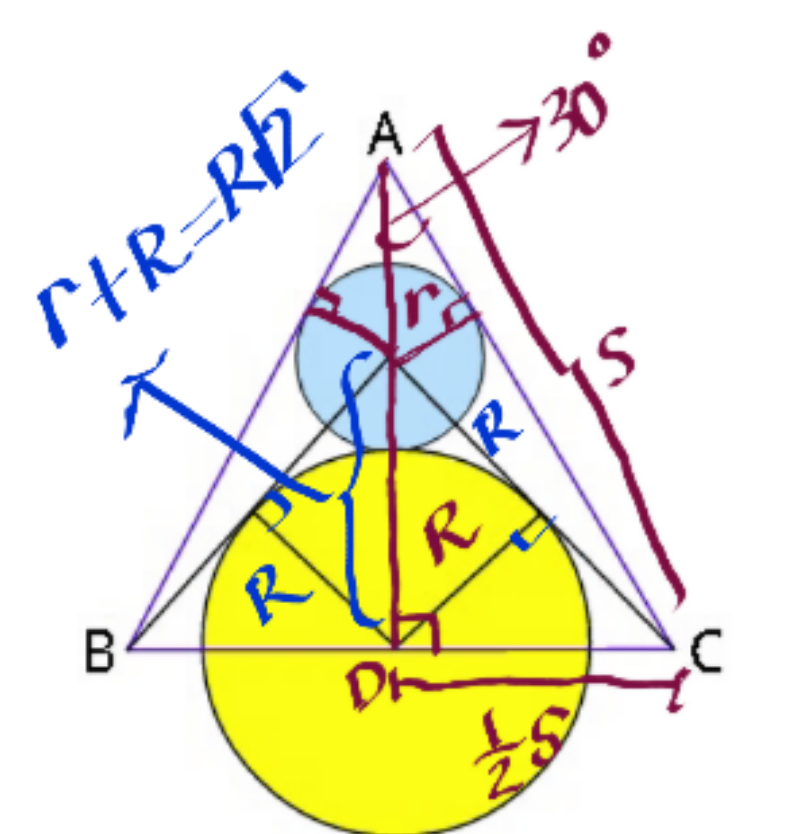
$${the}\:{quadrilateral}\:{isn}'{t}\:{a}\: \\ $$$${parallelogram},\:\:{wrong}.. \\ $$
Commented by bramlex last updated on 11/Jul/20

$$\mathrm{no}. \\ $$
Answered by mr W last updated on 11/Jul/20
Commented by mr W last updated on 11/Jul/20

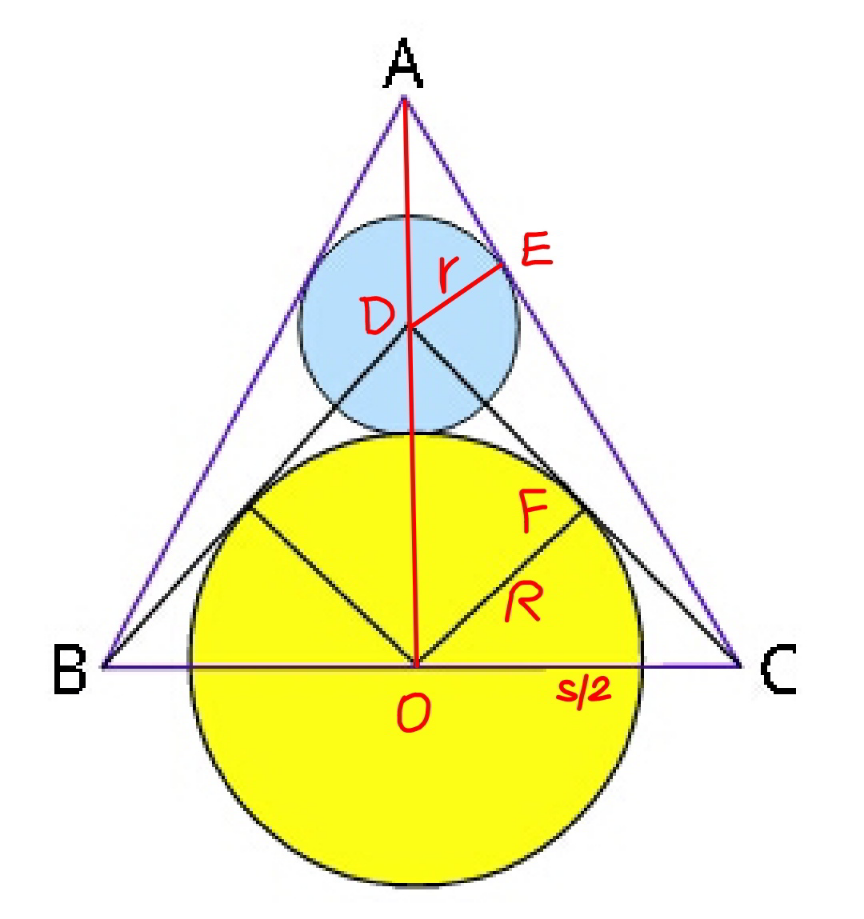
$${CF}=\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{4}}−{R}^{\mathrm{2}} } \\ $$$$\frac{{OD}}{{OC}}=\frac{{OF}}{{CF}} \\ $$$$\Rightarrow{OD}=\frac{{sR}}{\sqrt{{s}^{\mathrm{2}} −\mathrm{4}{R}^{\mathrm{2}} }} \\ $$$${r}={OD}−{R}=\left(\frac{{s}}{\sqrt{{s}^{\mathrm{2}} −\mathrm{4}{R}^{\mathrm{2}} }}−\mathrm{1}\right){R} \\ $$$${OA}={R}+\mathrm{3}{r}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}} \\ $$$${R}+\mathrm{3}\left(\frac{{sR}}{\sqrt{{s}^{\mathrm{2}} −\mathrm{4}{R}^{\mathrm{2}} }}−{R}\right)=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}} \\ $$$${with}\:\lambda=\frac{{R}}{{s}} \\ $$$$\Rightarrow\frac{\mathrm{3}}{\sqrt{\mathrm{1}−\mathrm{4}\lambda^{\mathrm{2}} }}=\mathrm{2}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\lambda} \\ $$$$\Rightarrow\mathrm{64}\lambda^{\mathrm{4}} +\mathrm{32}\sqrt{\mathrm{3}}\lambda^{\mathrm{3}} +\mathrm{32}\lambda^{\mathrm{2}} −\mathrm{8}\sqrt{\mathrm{3}}\lambda−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{R}}{{s}}\approx\mathrm{0}.\mathrm{3642} \\ $$$$\Rightarrow\frac{{r}}{{s}}=\left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{4}\lambda^{\mathrm{2}} }}−\mathrm{1}\right)\lambda\approx\mathrm{0}.\mathrm{1674} \\ $$
Commented by mr W last updated on 11/Jul/20
Commented by ajfour last updated on 11/Jul/20
$${Very}\:{Nice}\:{solution}\:{Sir};\:{Thanks}! \\ $$
Answered by 1549442205 last updated on 11/Jul/20
Commented by 1549442205 last updated on 11/Jul/20

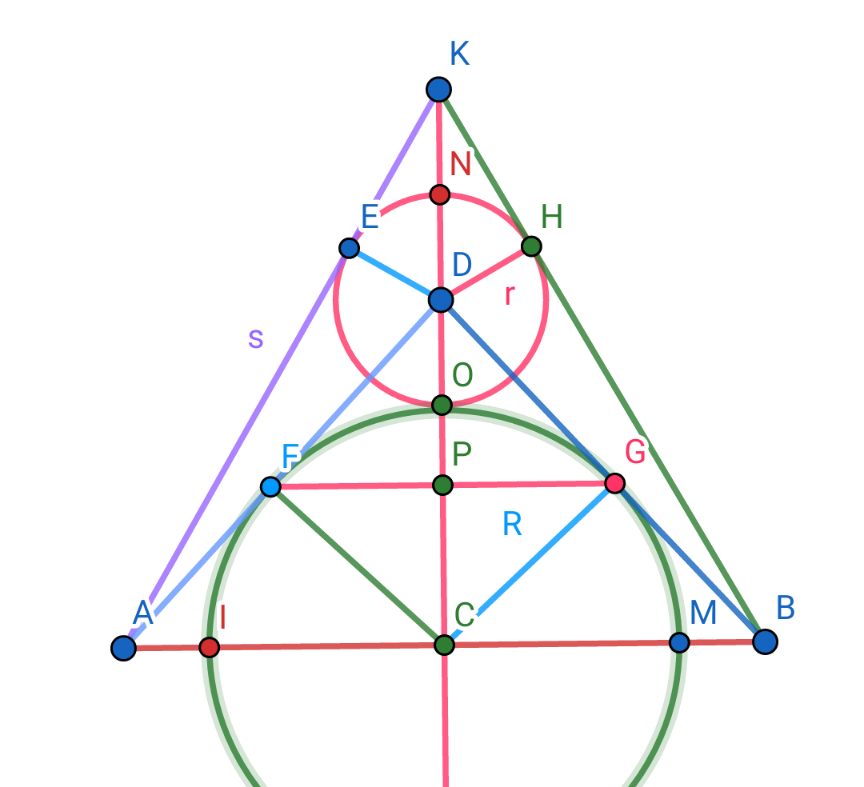
$$\mathrm{Since}\:\widehat {\mathrm{DKE}}=\mathrm{30}°,\mathrm{KD}=\frac{\mathrm{DE}}{\mathrm{sin}\widehat {\mathrm{DKE}}}=\frac{\mathrm{r}}{\mathrm{sin30}°} \\ $$$$\Rightarrow\mathrm{KD}=\mathrm{2r}.\mathrm{We}\:\mathrm{have}\:\mathrm{KC}=\mathrm{KAcos30}°=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$,\mathrm{so}\:\mathrm{KD}=\mathrm{KC}−\mathrm{CD}.\mathrm{Hence}, \\ $$$$\mathrm{2r}=\frac{\mathrm{s}\sqrt{\mathrm{3}}}{\mathrm{2}}−\left(\mathrm{R}+\mathrm{r}\right)\Leftrightarrow\mathrm{r}=\frac{\mathrm{s}\sqrt{\mathrm{3}}−\mathrm{2R}}{\mathrm{6}}\left(\mathrm{1}\right) \\ $$$$\mathrm{On}\:\mathrm{ther}\:\mathrm{other}\:\mathrm{hands}, \\ $$$$\mathrm{AD}^{\mathrm{2}} =\left(\mathrm{R}+\mathrm{r}\right)^{\mathrm{2}} +\frac{\mathrm{s}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{KE}=\mathrm{r}\sqrt{\mathrm{3}}\:\mathrm{and}\:\mathrm{AE}=\mathrm{s}−\mathrm{KE}=\mathrm{s}−\mathrm{r}\sqrt{\mathrm{3}}\:, \\ $$$$\mathrm{AE}^{\mathrm{2}} +\mathrm{DE}^{\mathrm{2}} =\mathrm{AD}^{\mathrm{2}} =\mathrm{DC}^{\mathrm{2}} +\mathrm{AC}^{\mathrm{2}} ,\mathrm{so} \\ $$$$\left(\mathrm{s}−\mathrm{r}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\left(\mathrm{R}+\mathrm{r}\right)^{\mathrm{2}} +\frac{\mathrm{s}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{R}^{\mathrm{2}} +\mathrm{2Rr}−\mathrm{3r}^{\mathrm{2}} +\mathrm{2sr}\sqrt{\mathrm{3}}−\frac{\mathrm{3s}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0}\left(\mathrm{due}\:\mathrm{to}\:\left(\mathrm{1}\right)\right) \\ $$$$\Leftrightarrow\mathrm{R}^{\mathrm{2}} +\frac{\mathrm{s}\sqrt{\mathrm{3}}−\mathrm{2R}}{\mathrm{3}}\left(\mathrm{R}+\mathrm{s}\sqrt{\mathrm{3}}\right)−\frac{\mathrm{3s}^{\mathrm{2}} −\mathrm{4Rs}\sqrt{\mathrm{3}}+\mathrm{4R}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{3s}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{4R}^{\mathrm{2}} −\mathrm{12Rs}\sqrt{\mathrm{3}}\:+\mathrm{9s}^{\mathrm{2}} =\mathrm{0}\:\:.\Delta'=\mathrm{108s}^{\mathrm{2}} −\mathrm{36s}^{\mathrm{2}} =\mathrm{72s}^{\mathrm{2}} \\ $$$$\mathrm{R}=\frac{\mathrm{6}\boldsymbol{\mathrm{s}}\sqrt{\mathrm{3}}−\mathrm{6}\boldsymbol{\mathrm{s}}\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\mathrm{3}\boldsymbol{\mathrm{s}}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)}{\mathrm{2}}.\mathrm{Replace} \\ $$$$\mathrm{into}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\:\boldsymbol{\mathrm{r}}=\frac{\boldsymbol{\mathrm{s}}\sqrt{\mathrm{3}}−\mathrm{3}\boldsymbol{\mathrm{s}}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)}{\mathrm{6}}=\frac{\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}\right)\boldsymbol{\mathrm{s}}}{\mathrm{6}} \\ $$$$\mathrm{Thus},\begin{cases}{\frac{\mathrm{R}}{\mathrm{s}}=\frac{\mathrm{3}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\approx\mathrm{0}.\mathrm{47675586}}\\{\frac{\mathrm{r}}{\mathrm{s}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{6}}\approx\mathrm{0}.\mathrm{12975512}}\end{cases} \\ $$
