
Question Number 102508 by Study last updated on 09/Jul/20
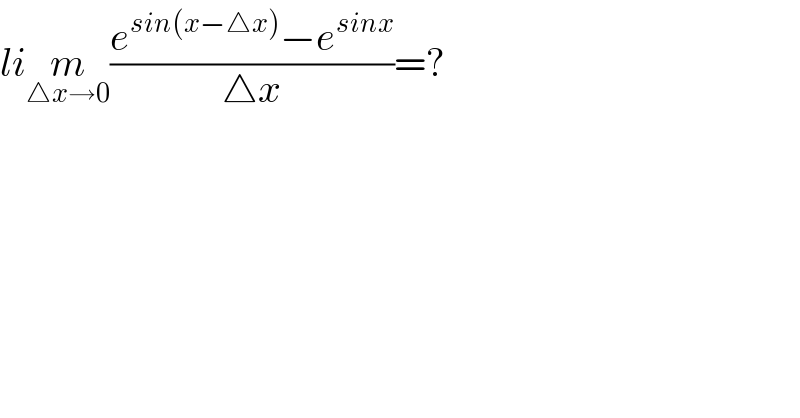
$${li}\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {{m}}\frac{{e}^{{sin}\left({x}−\bigtriangleup{x}\right)} −{e}^{{sinx}} }{\bigtriangleup{x}}=? \\ $$
Commented by bemath last updated on 09/Jul/20
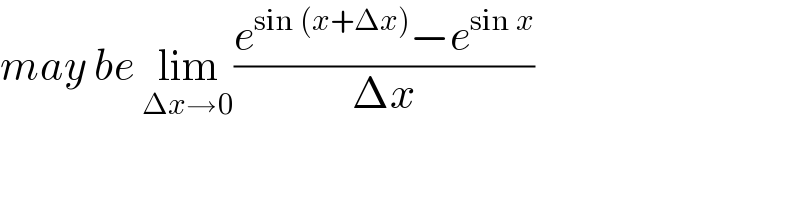
$${may}\:{be}\:\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{sin}\:\left({x}+\Delta{x}\right)} −{e}^{\mathrm{sin}\:{x}} }{\Delta{x}} \\ $$
Commented by Study last updated on 09/Jul/20

$${no}\:{sir} \\ $$
Commented by Study last updated on 09/Jul/20

$${help}\:{me} \\ $$
Commented by bemath last updated on 09/Jul/20

$${using}\:{LHopital} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Jul/20
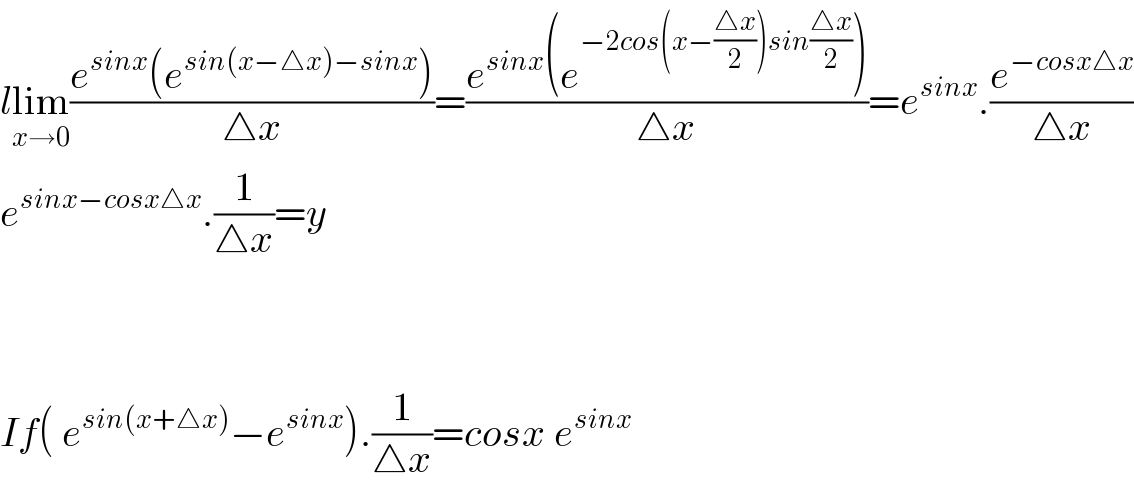
$${l}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{sinx}} \left({e}^{{sin}\left({x}−\bigtriangleup{x}\right)−{sinx}} \right)}{\bigtriangleup{x}}=\frac{{e}^{{sinx}} \left({e}^{−\mathrm{2}{cos}\left({x}−\frac{\bigtriangleup{x}}{\mathrm{2}}\right){sin}\frac{\bigtriangleup{x}}{\mathrm{2}}} \right)}{\bigtriangleup{x}}={e}^{{sinx}} .\frac{{e}^{−{cosx}\bigtriangleup{x}} }{\bigtriangleup{x}} \\ $$$${e}^{{sinx}−{cosx}\bigtriangleup{x}} .\frac{\mathrm{1}}{\bigtriangleup{x}}={y} \\ $$$$ \\ $$$$ \\ $$$${If}\left(\:{e}^{{sin}\left({x}+\bigtriangleup{x}\right)} −{e}^{{sinx}} \right).\frac{\mathrm{1}}{\bigtriangleup{x}}={cosx}\:{e}^{{sinx}} \\ $$
