
Previous in Differential Equation Next in Differential Equation
Question Number 102382 by Ar Brandon last updated on 08/Jul/20
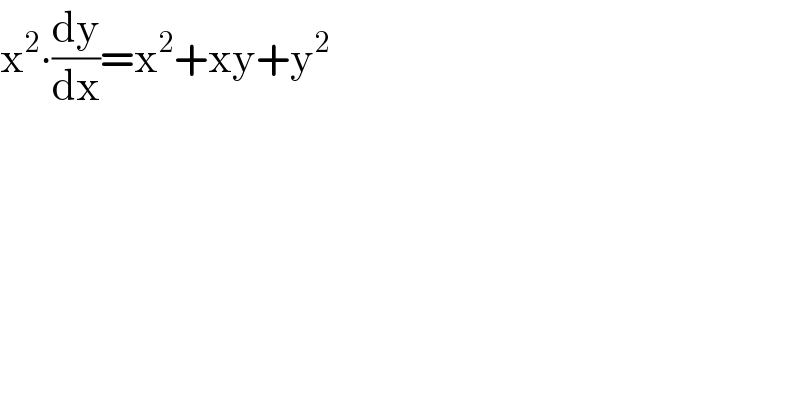
$$\mathrm{x}^{\mathrm{2}} \centerdot\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{x}^{\mathrm{2}} +\mathrm{xy}+\mathrm{y}^{\mathrm{2}} \\ $$
Answered by PRITHWISH SEN 2 last updated on 08/Jul/20
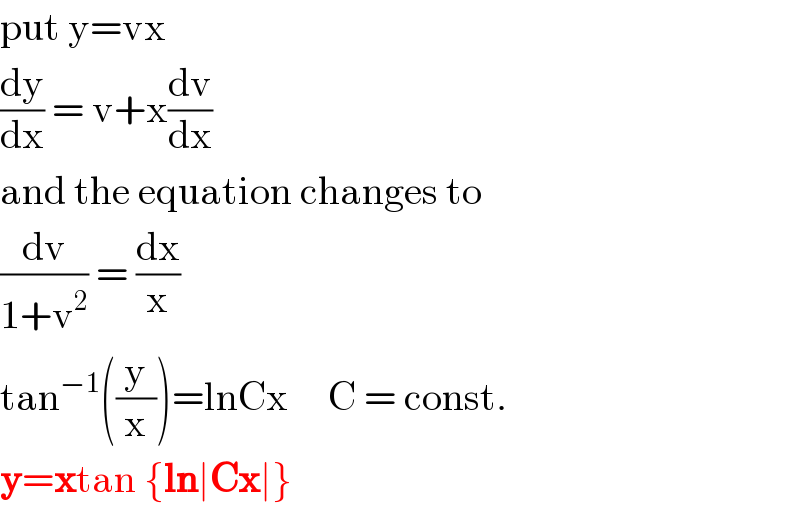
$$\mathrm{put}\:\mathrm{y}=\mathrm{vx} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{v}+\mathrm{x}\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{changes}\:\mathrm{to} \\ $$$$\frac{\mathrm{dv}}{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\:=\:\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{y}}{\mathrm{x}}\right)=\mathrm{lnCx}\:\:\:\:\:\mathrm{C}\:=\:\mathrm{const}. \\ $$$$\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{x}}\mathrm{tan}\:\left\{\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{Cx}}\mid\right\} \\ $$
Commented by Ar Brandon last updated on 08/Jul/20
Oh thanks, I didn't notice that.
