
Question Number 102296 by bemath last updated on 08/Jul/20
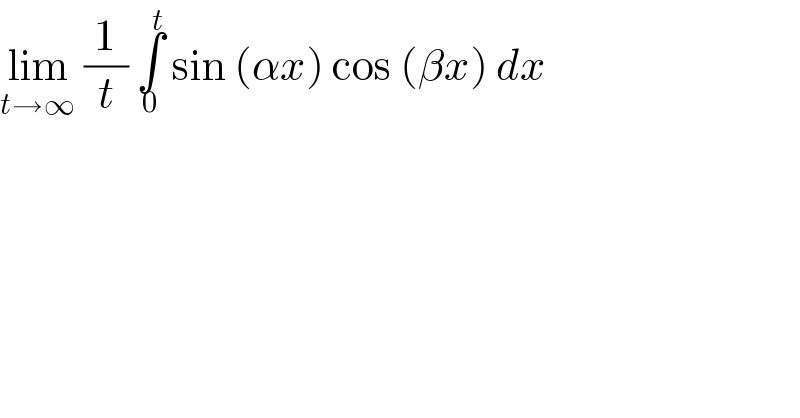
$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{t}}\:\underset{\mathrm{0}} {\overset{{t}} {\int}}\:\mathrm{sin}\:\left(\alpha{x}\right)\:\mathrm{cos}\:\left(\beta{x}\right)\:{dx} \\ $$
Answered by john santu last updated on 08/Jul/20
![assume α,β > 0 lim_(t→∞) (1/t)∫_0 ^t sin (αx)cos (βx)dx lim_(t→∞) (1/(2t))∫_0 ^t sin (α+β)x+sin (α−β)x dx lim_(t→∞) −(1/(2t)) [((cos (α+β)x)/(α+β)) + ((cos (α−β)x)/(α−β)) ]_0 ^t lim_(t→∞) ((cos (α+β)t)/(−2(α+β)t)) + lim_(t→∞) ((cos (α−β)t)/(−2(α−β)t)) = 0 (JS ⊛)](Q102299.png)
$${assume}\:\alpha,\beta\:>\:\mathrm{0} \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{{t}} \mathrm{sin}\:\left(\alpha{x}\right)\mathrm{cos}\:\left(\beta{x}\right){dx} \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}{t}}\int_{\mathrm{0}} ^{{t}} \:\mathrm{sin}\:\left(\alpha+\beta\right){x}+\mathrm{sin}\:\left(\alpha−\beta\right){x}\:{dx} \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\:−\frac{\mathrm{1}}{\mathrm{2}{t}}\:\left[\frac{\mathrm{cos}\:\left(\alpha+\beta\right){x}}{\alpha+\beta}\:+\:\frac{\mathrm{cos}\:\left(\alpha−\beta\right){x}}{\alpha−\beta}\:\right]_{\mathrm{0}} ^{{t}} \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\alpha+\beta\right){t}}{−\mathrm{2}\left(\alpha+\beta\right){t}}\:+\:\underset{{t}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\alpha−\beta\right){t}}{−\mathrm{2}\left(\alpha−\beta\right){t}}\:=\:\mathrm{0} \\ $$$$\left({JS}\:\circledast\right) \\ $$$$ \\ $$
