
Question Number 102178 by dw last updated on 07/Jul/20
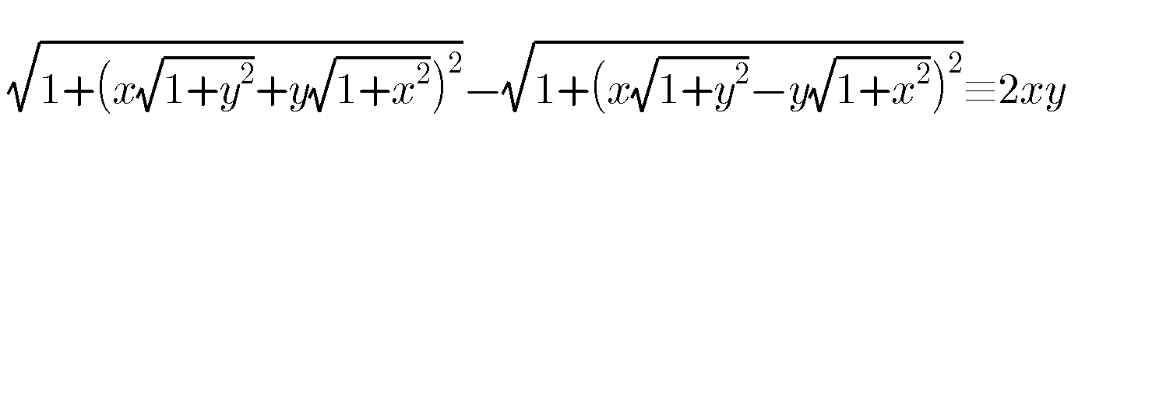
Answered by 1549442205 last updated on 07/Jul/20
![Putting x=tanα,y=tanβ we have (√(1+x^2 ))=(√(1+tan^2 α))=(1/(cosα)),(√(1+y^2 ))=(1/(cosβ)) x(√(1+y^2 ))+y(√(1+x^2 ))=((tamα)/(cosβ))+((tanβ)/(cosα))=((sinα+sinβ)/(cosαcosβ)).Hence, LHS=(1/(cosαcosβ))(√(1+(((sinα+sinβ)/(cosαcosβ)))^2 ))+(1/(cosαcosβ))(√(1+(((sinα−sinβ)/(cosαcosβ)))^2 )) =(1/(cosαcosβ))(√(cos^2 αcos^2 β+(sinα+sinβ)^2 ))+(1/(cosαcosβ))(√(cos^2 αcos^2 β+(sinα−sinβ)^2 )) we have :cos^2 αcos^2 β=(1−sin^2 α)(1−sin^2 β) =1+sin^2 αsin^2 β−sin^2 α−sin^2 β,so =(√(cos^2 αcos^2 β+(sinα+sinβ)^2 ))=(√(1+sin^2 αsin^2 β+2sinαsinβ)) =(√((sinαsinβ+1)^2 )) =1+sinαsinβ Similarly,=(√(cos^2 αcos^2 β+(sinα−sinβ)^2 ))=1−sinαsinβ Therefore,LHS=(1/(cosαcosβ))[(1+sinαsinβ)−(1−sinαsinβ)] =((2sinαsinβ)/(cosαcosβ))=2tanαtanβ=2xy Thus,LHS=RHS(q.e.d)](Q102188.png)
$$\mathrm{Putting}\:\mathrm{x}=\mathrm{tan}\alpha,\mathrm{y}=\mathrm{tan}\beta\:\mathrm{we}\:\mathrm{have} \\ $$$$\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \alpha}=\frac{\mathrm{1}}{\mathrm{cos}\alpha},\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{cos}\beta} \\ $$$$\mathrm{x}\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }+\mathrm{y}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{tam}\alpha}{\mathrm{cos}\beta}+\frac{\mathrm{tan}\beta}{\mathrm{cos}\alpha}=\frac{\mathrm{sin}\alpha+\mathrm{sin}\beta}{\mathrm{cos}\alpha\mathrm{cos}\beta}.\mathrm{Hence}, \\ $$$$\mathrm{LHS}=\frac{\mathrm{1}}{\mathrm{cos}\alpha\mathrm{cos}\beta}\sqrt{\mathrm{1}+\left(\frac{\mathrm{sin}\alpha+\mathrm{sin}\beta}{\mathrm{cos}\alpha\mathrm{cos}\beta}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{cos}\alpha\mathrm{cos}\beta}\sqrt{\mathrm{1}+\left(\frac{\mathrm{sin}\alpha−\mathrm{sin}\beta}{\mathrm{cos}\alpha\mathrm{cos}\beta}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}\alpha\mathrm{cos}\beta}\sqrt{\mathrm{cos}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \beta+\left(\mathrm{sin}\alpha+\mathrm{sin}\beta\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{cos}\alpha\mathrm{cos}\beta}\sqrt{\mathrm{cos}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \beta+\left(\mathrm{sin}\alpha−\mathrm{sin}\beta\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\::\mathrm{cos}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \beta=\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \alpha\right)\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \beta\right) \\ $$$$=\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \alpha\mathrm{sin}^{\mathrm{2}} \beta−\mathrm{sin}^{\mathrm{2}} \alpha−\mathrm{sin}^{\mathrm{2}} \beta,\mathrm{so} \\ $$$$=\sqrt{\mathrm{cos}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \beta+\left(\mathrm{sin}\alpha+\mathrm{sin}\beta\right)^{\mathrm{2}} \:}=\sqrt{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \alpha\mathrm{sin}^{\mathrm{2}} \beta+\mathrm{2sin}\alpha\mathrm{sin}\beta} \\ $$$$=\sqrt{\left(\mathrm{sin}\alpha\mathrm{sin}\beta+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{1}+\mathrm{sin}\alpha\mathrm{sin}\beta \\ $$$$\mathrm{Similarly},=\sqrt{\mathrm{cos}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \beta+\left(\mathrm{sin}\alpha−\mathrm{sin}\beta\right)^{\mathrm{2}} }=\mathrm{1}−\mathrm{sin}\alpha\mathrm{sin}\beta \\ $$$$\mathrm{Therefore},\mathrm{LHS}=\frac{\mathrm{1}}{\mathrm{cos}\alpha\mathrm{cos}\beta}\left[\left(\mathrm{1}+\mathrm{sin}\alpha\mathrm{sin}\beta\right)−\left(\mathrm{1}−\mathrm{sin}\alpha\mathrm{sin}\beta\right)\right] \\ $$$$=\frac{\mathrm{2sin}\alpha\mathrm{sin}\beta}{\mathrm{cos}\alpha\mathrm{cos}\beta}=\mathrm{2tan}\alpha\mathrm{tan}\beta=\mathrm{2xy} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{LHS}}=\boldsymbol{\mathrm{RHS}}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$$$ \\ $$
Commented by dw last updated on 07/Jul/20
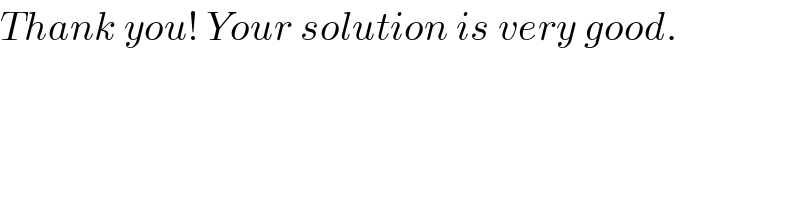
$${Thank}\:{you}!\:{Your}\:{solution}\:{is}\:{very}\:{good}. \\ $$
Commented by dw last updated on 16/Jul/20
![but I did not understand ! (1/(cosαcosβ))[(1+sinαsinβ)−(1−sinαsinβ)]= (1/(cosαcosβ))[(1+sinαsinβ)+(1−sinαsinβ)](Q103653.png)
$${but}\:{I}\:{did}\:{not}\:{understand}\:! \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{cos}\alpha{cos}\beta}\left[\left(\mathrm{1}+{sin}\alpha{sin}\beta\right)−\left(\mathrm{1}−{sin}\alpha{sin}\beta\right)\right]= \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{cos}\alpha{cos}\beta}\left[\left(\mathrm{1}+{sin}\alpha{sin}\beta\right)+\left(\mathrm{1}−{sin}\alpha{sin}\beta\right)\right. \\ $$$$ \\ $$
