
Question Number 102121 by Rohit@Thakur last updated on 06/Jul/20
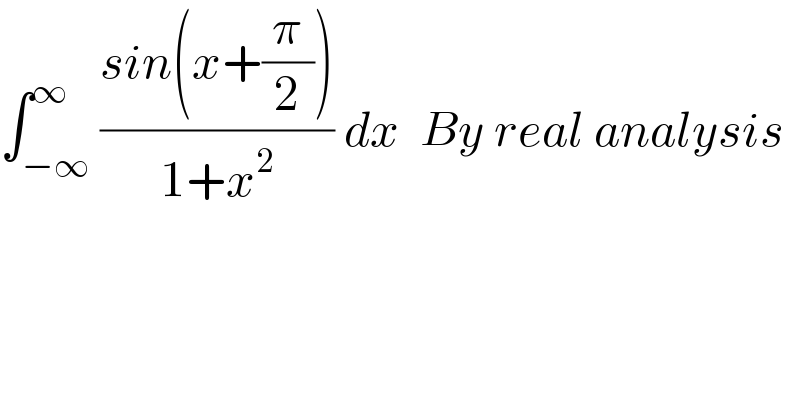
$$\int_{−\infty} ^{\infty} \frac{{sin}\left({x}+\frac{\pi}{\mathrm{2}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\:{By}\:{real}\:{analysis} \\ $$
Commented by prakash jain last updated on 06/Jul/20
https://youtu.be/YWBdwYr6PGg Solution video.
Answered by Ar Brandon last updated on 06/Jul/20
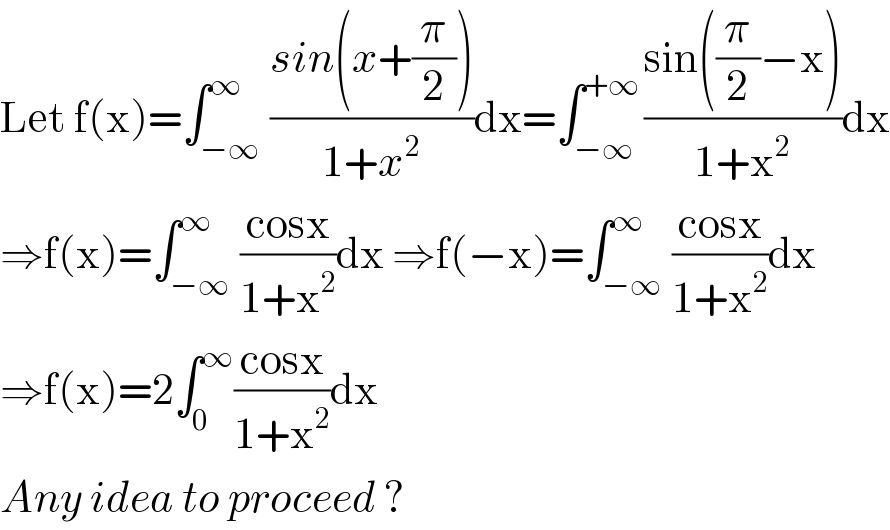
$$\mathrm{Let}\:\mathrm{f}\left(\mathrm{x}\right)=\int_{−\infty} ^{\infty} \frac{{sin}\left({x}+\frac{\pi}{\mathrm{2}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{dx}=\int_{−\infty} ^{+\infty} \frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\int_{−\infty} ^{\infty} \frac{\mathrm{cosx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}\left(−\mathrm{x}\right)=\int_{−\infty} ^{\infty} \frac{\mathrm{cosx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cosx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$${Any}\:{idea}\:{to}\:{proceed}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jul/20
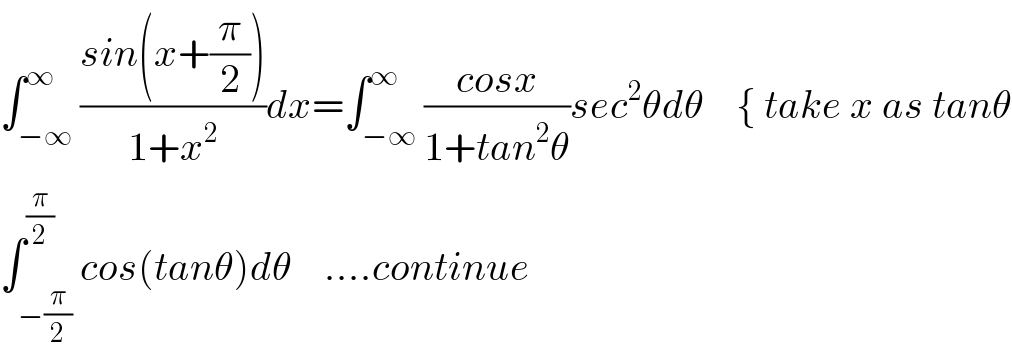
$$\int_{−\infty} ^{\infty} \frac{{sin}\left({x}+\frac{\pi}{\mathrm{2}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{−\infty} ^{\infty} \frac{{cosx}}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{sec}^{\mathrm{2}} \theta{d}\theta\:\:\:\:\left\{\:{take}\:{x}\:{as}\:{tan}\theta\right. \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left({tan}\theta\right){d}\theta\:\:\:\:....{continue} \\ $$
Answered by mathmax by abdo last updated on 06/Jul/20

$$\mathrm{sir}\:\mathrm{rohit}\:\mathrm{want}\:\mathrm{real}\:\mathrm{method}...! \\ $$
Commented by prakash jain last updated on 06/Jul/20

$$\mathrm{Yez}.\:\mathrm{I}\:\mathrm{had}\:\mathrm{this}\:\mathrm{vidro}\:\mathrm{link}\:\mathrm{saved}\:\mathrm{so} \\ $$$$\mathrm{i}\:\mathrm{shared}\:\mathrm{it}\:\mathrm{anyway}. \\ $$
