
Question Number 10212 by konen last updated on 30/Jan/17
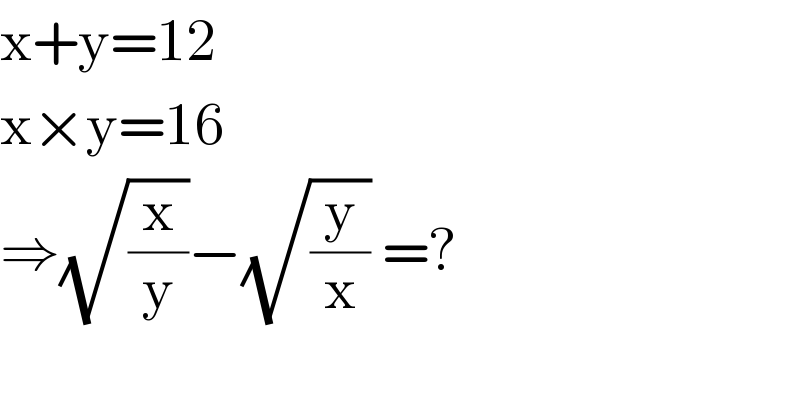
$$\mathrm{x}+\mathrm{y}=\mathrm{12} \\ $$$$\mathrm{x}×\mathrm{y}=\mathrm{16} \\ $$$$\Rightarrow\sqrt{\frac{\mathrm{x}}{\mathrm{y}}}−\sqrt{\frac{\mathrm{y}}{\mathrm{x}}}\:=? \\ $$
Answered by ridwan balatif last updated on 30/Jan/17
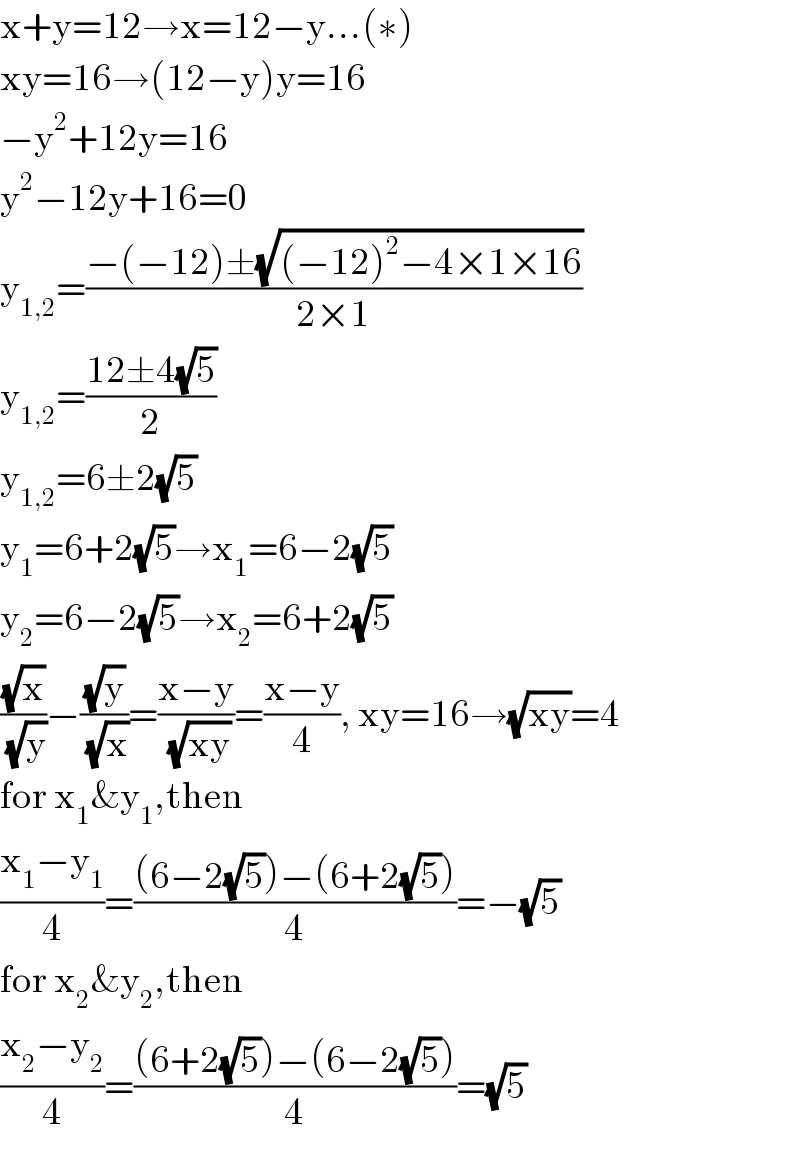
$$\mathrm{x}+\mathrm{y}=\mathrm{12}\rightarrow\mathrm{x}=\mathrm{12}−\mathrm{y}...\left(\ast\right) \\ $$$$\mathrm{xy}=\mathrm{16}\rightarrow\left(\mathrm{12}−\mathrm{y}\right)\mathrm{y}=\mathrm{16} \\ $$$$−\mathrm{y}^{\mathrm{2}} +\mathrm{12y}=\mathrm{16} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{12y}+\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{1},\mathrm{2}} =\frac{−\left(−\mathrm{12}\right)\pm\sqrt{\left(−\mathrm{12}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\mathrm{16}}}{\mathrm{2}×\mathrm{1}} \\ $$$$\mathrm{y}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{12}\pm\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{y}_{\mathrm{1},\mathrm{2}} =\mathrm{6}\pm\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{y}_{\mathrm{1}} =\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\rightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{y}_{\mathrm{2}} =\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\rightarrow\mathrm{x}_{\mathrm{2}} =\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\frac{\sqrt{\mathrm{x}}}{\sqrt{\mathrm{y}}}−\frac{\sqrt{\mathrm{y}}}{\sqrt{\mathrm{x}}}=\frac{\mathrm{x}−\mathrm{y}}{\sqrt{\mathrm{xy}}}=\frac{\mathrm{x}−\mathrm{y}}{\mathrm{4}},\:\mathrm{xy}=\mathrm{16}\rightarrow\sqrt{\mathrm{xy}}=\mathrm{4} \\ $$$$\mathrm{for}\:\mathrm{x}_{\mathrm{1}} \&\mathrm{y}_{\mathrm{1}} ,\mathrm{then} \\ $$$$\frac{\mathrm{x}_{\mathrm{1}} −\mathrm{y}_{\mathrm{1}} }{\mathrm{4}}=\frac{\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\right)−\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{4}}=−\sqrt{\mathrm{5}} \\ $$$$\mathrm{for}\:\mathrm{x}_{\mathrm{2}} \&\mathrm{y}_{\mathrm{2}} ,\mathrm{then} \\ $$$$\frac{\mathrm{x}_{\mathrm{2}} −\mathrm{y}_{\mathrm{2}} }{\mathrm{4}}=\frac{\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\right)−\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\right)}{\mathrm{4}}=\sqrt{\mathrm{5}} \\ $$
Answered by nume1114 last updated on 30/Jan/17
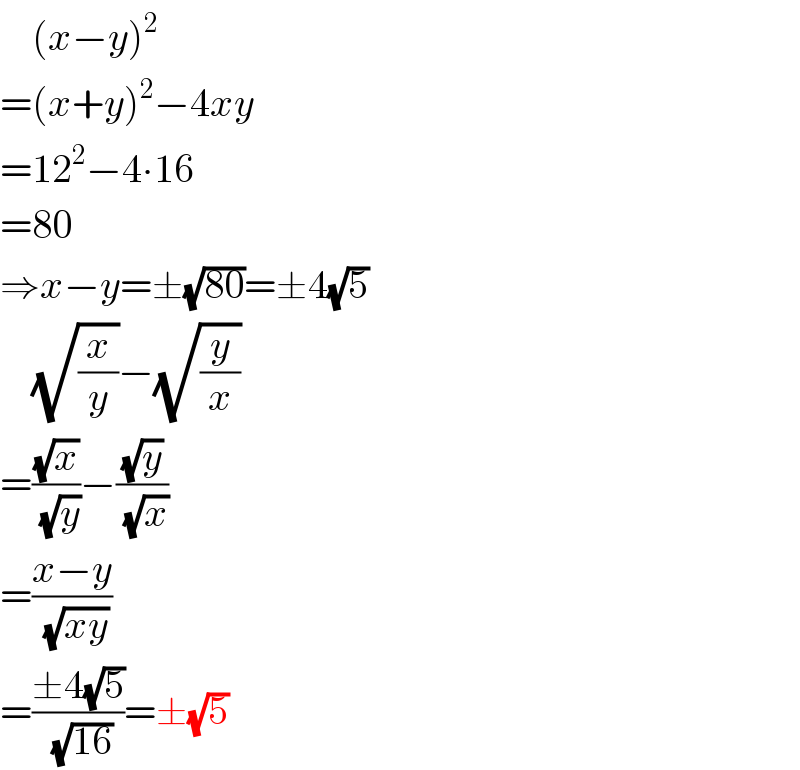
$$\:\:\:\:\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$=\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy} \\ $$$$=\mathrm{12}^{\mathrm{2}} −\mathrm{4}\centerdot\mathrm{16} \\ $$$$=\mathrm{80} \\ $$$$\Rightarrow{x}−{y}=\pm\sqrt{\mathrm{80}}=\pm\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:\sqrt{\frac{{x}}{{y}}}−\sqrt{\frac{{y}}{{x}}} \\ $$$$=\frac{\sqrt{{x}}}{\sqrt{{y}}}−\frac{\sqrt{{y}}}{\sqrt{{x}}} \\ $$$$=\frac{{x}−{y}}{\sqrt{{xy}}} \\ $$$$=\frac{\pm\mathrm{4}\sqrt{\mathrm{5}}}{\sqrt{\mathrm{16}}}=\pm\sqrt{\mathrm{5}} \\ $$
Answered by arge last updated on 04/Feb/17
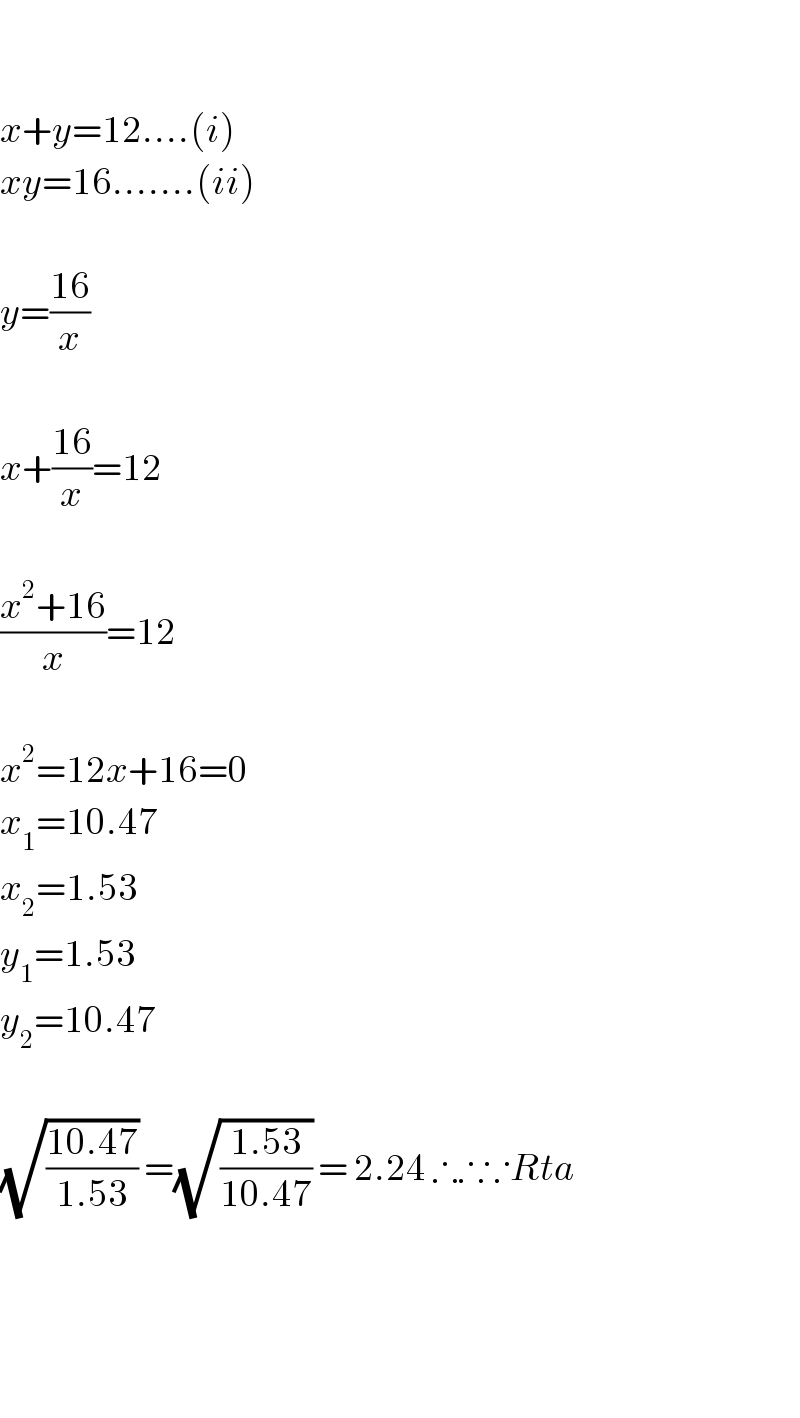
$$ \\ $$$$ \\ $$$${x}+{y}=\mathrm{12}....\left({i}\right) \\ $$$${xy}=\mathrm{16}.......\left({ii}\right) \\ $$$$ \\ $$$${y}=\frac{\mathrm{16}}{{x}} \\ $$$$ \\ $$$${x}+\frac{\mathrm{16}}{{x}}=\mathrm{12} \\ $$$$ \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{16}}{{x}}=\mathrm{12} \\ $$$$ \\ $$$${x}^{\mathrm{2}} =\mathrm{12}{x}+\mathrm{16}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{10}.\mathrm{47} \\ $$$${x}_{\mathrm{2}} =\mathrm{1}.\mathrm{53} \\ $$$${y}_{\mathrm{1}} =\mathrm{1}.\mathrm{53} \\ $$$${y}_{\mathrm{2}} =\mathrm{10}.\mathrm{47} \\ $$$$ \\ $$$$\sqrt{\frac{\mathrm{10}.\mathrm{47}}{\mathrm{1}.\mathrm{53}}}\:=\sqrt{\frac{\mathrm{1}.\mathrm{53}}{\mathrm{10}.\mathrm{47}}}\:=\:\mathrm{2}.\mathrm{24}\:\therefore\therefore\because{Rta} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
