
Question Number 102099 by Study last updated on 06/Jul/20
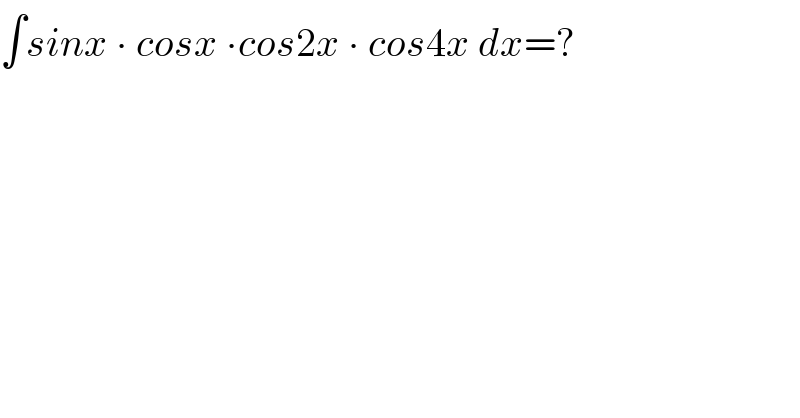
$$\int{sinx}\:\centerdot\:{cosx}\:\centerdot{cos}\mathrm{2}{x}\:\centerdot\:{cos}\mathrm{4}{x}\:{dx}=? \\ $$
Answered by PRITHWISH SEN 2 last updated on 06/Jul/20
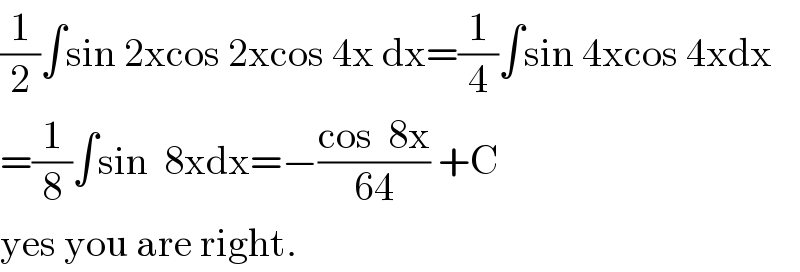
$$\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\:\mathrm{2xcos}\:\mathrm{2xcos}\:\mathrm{4x}\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{sin}\:\mathrm{4xcos}\:\mathrm{4xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{sin}\:\:\mathrm{8xdx}=−\frac{\mathrm{cos}\:\:\mathrm{8x}}{\mathrm{64}}\:+\mathrm{C} \\ $$$$\mathrm{yes}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}. \\ $$
Commented by Study last updated on 06/Jul/20
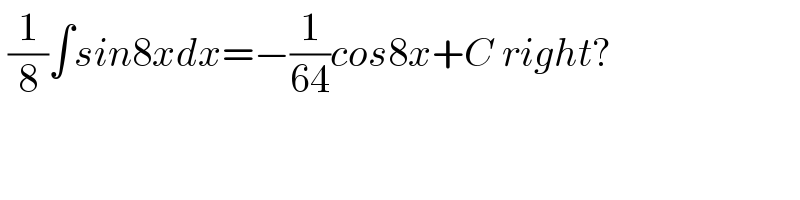
$$\:\frac{\mathrm{1}}{\mathrm{8}}\int{sin}\mathrm{8}{xdx}=−\frac{\mathrm{1}}{\mathrm{64}}{cos}\mathrm{8}{x}+{C}\:{right}? \\ $$
