Question Number 101851 by bemath last updated on 05/Jul/20
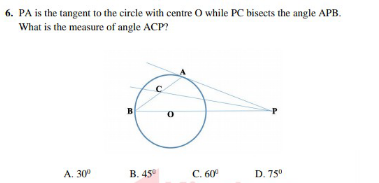
Answered by bobhans last updated on 05/Jul/20
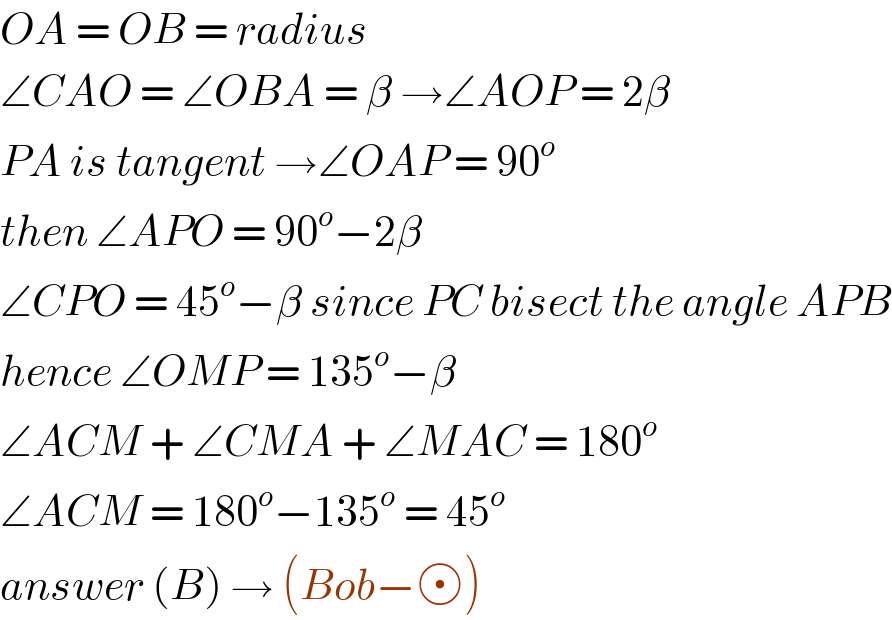
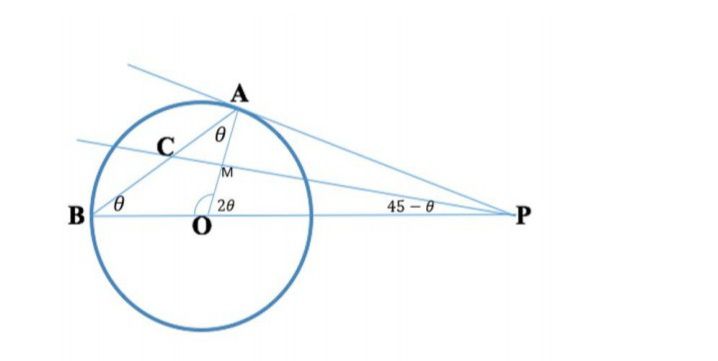
$${OA}\:=\:{OB}\:=\:{radius} \\ $$$$\angle{CAO}\:=\:\angle{OBA}\:=\:\beta\:\rightarrow\angle{AOP}\:=\:\mathrm{2}\beta \\ $$$${PA}\:{is}\:{tangent}\:\rightarrow\angle{OAP}\:=\:\mathrm{90}^{{o}} \\ $$$${then}\:\angle{APO}\:=\:\mathrm{90}^{{o}} −\mathrm{2}\beta\: \\ $$$$\angle{CPO}\:=\:\mathrm{45}^{{o}} −\beta\:{since}\:{PC}\:{bisect}\:{the}\:{angle}\:{APB} \\ $$$${hence}\:\angle{OMP}\:=\:\mathrm{135}^{{o}} −\beta \\ $$$$\angle{ACM}\:+\:\angle{CMA}\:+\:\angle{MAC}\:=\:\mathrm{180}^{{o}} \\ $$$$\angle{ACM}\:=\:\mathrm{180}^{{o}} −\mathrm{135}^{{o}} \:=\:\mathrm{45}^{{o}} \: \\ $$$${answer}\:\left({B}\right)\:\rightarrow\:\left({Bob}− \right) \\ $$
Commented by bemath last updated on 05/Jul/20
coll....♡♥~♥~
Commented by bobhans last updated on 05/Jul/20