
Question Number 101493 by bemath last updated on 03/Jul/20
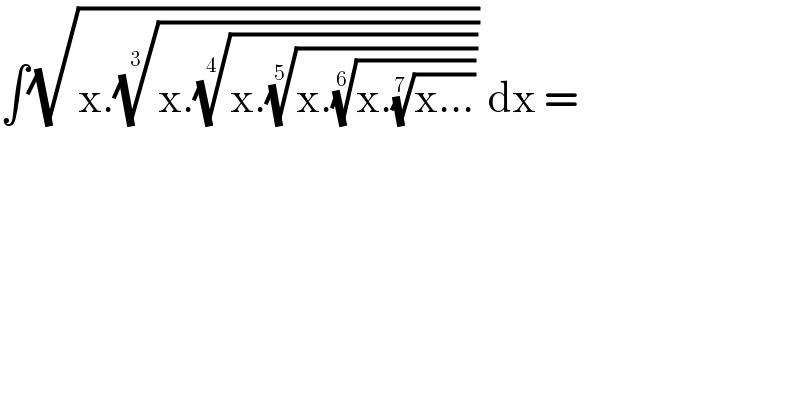
$$\int\sqrt{\mathrm{x}.\sqrt[{\mathrm{3}}]{\mathrm{x}.\sqrt[{\mathrm{4}}]{\mathrm{x}.\sqrt[{\mathrm{5}}]{\mathrm{x}.\sqrt[{\mathrm{6}}]{\mathrm{x}.\sqrt[{\mathrm{7}}]{\mathrm{x}...}}}}}}\:\mathrm{dx}\:=\: \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 03/Jul/20

$${let}'{s}\:{see}\:{a}\:{small}\:{case}\:{first}\:{to}\:{understand} \\ $$$${better}\:{whats}\:{going}\:{on} \\ $$$$\sqrt{{x}.\sqrt[{\mathrm{3}}]{{x}\sqrt[{\mathrm{4}}]{{x}}}}=\left({x}\left({x}\left({x}\right)^{\mathrm{1}/\mathrm{4}} \right)^{\mathrm{1}/\mathrm{3}} \right)^{\mathrm{1}/\mathrm{2}} ={x}^{\frac{\mathrm{1}}{\mathrm{2}}} .{x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}} .{x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$={x}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}.\mathrm{4}}} ={x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}} \\ $$$${so}\:{back}\:{to}\:{the}\:{initial}\:{problem},\:{we}\:{have}: \\ $$$$=\int{x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+...} {dx} \\ $$$${now}\:{we}\:{want}\:{to}\:{get}\:{a}\:{close}\:{form}\:{for}\:{this}\:{expression}\:{on}\:{the}\:{exponent}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+...=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$${from}\:{the}\:{taylor}\:{series}\:{expansion}\:{to}\:{e}^{{x}} \:{we}\:{have}\:{that} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${when}\:{x}=\mathrm{1}: \\ $$$${e}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{1}}{\mathrm{1}!}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\mathrm{2}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$$\Rightarrow\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}={e}−\mathrm{2} \\ $$$$\Rightarrow\int{x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+...} {dx}=\int{x}^{{e}−\mathrm{2}} {dx}=\frac{{x}^{{e}−\mathrm{1}} }{{e}−\mathrm{1}}+{C} \\ $$
Commented by 1549442205 last updated on 03/Jul/20

$$\mathrm{A}\:\mathrm{great}\:\mathrm{work}\:! \\ $$
Commented by bemath last updated on 03/Jul/20
coll ������
