
Question Number 10138 by konen last updated on 26/Jan/17
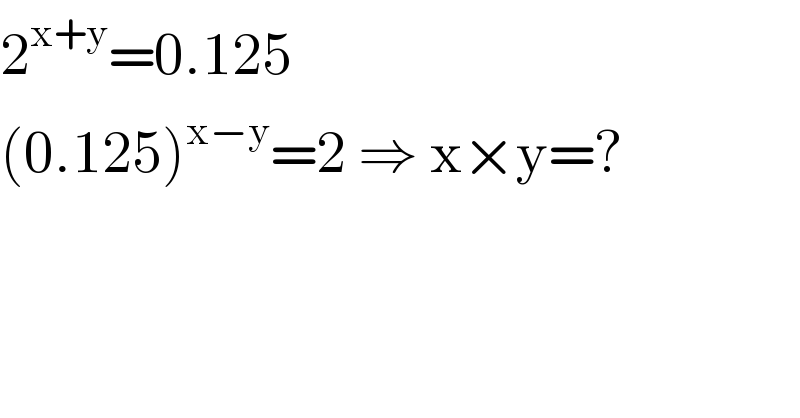
$$\mathrm{2}^{\mathrm{x}+\mathrm{y}} =\mathrm{0}.\mathrm{125} \\ $$$$\left(\mathrm{0}.\mathrm{125}\right)^{\mathrm{x}−\mathrm{y}} =\mathrm{2}\:\Rightarrow\:\mathrm{x}×\mathrm{y}=? \\ $$
Answered by sandy_suhendra last updated on 26/Jan/17
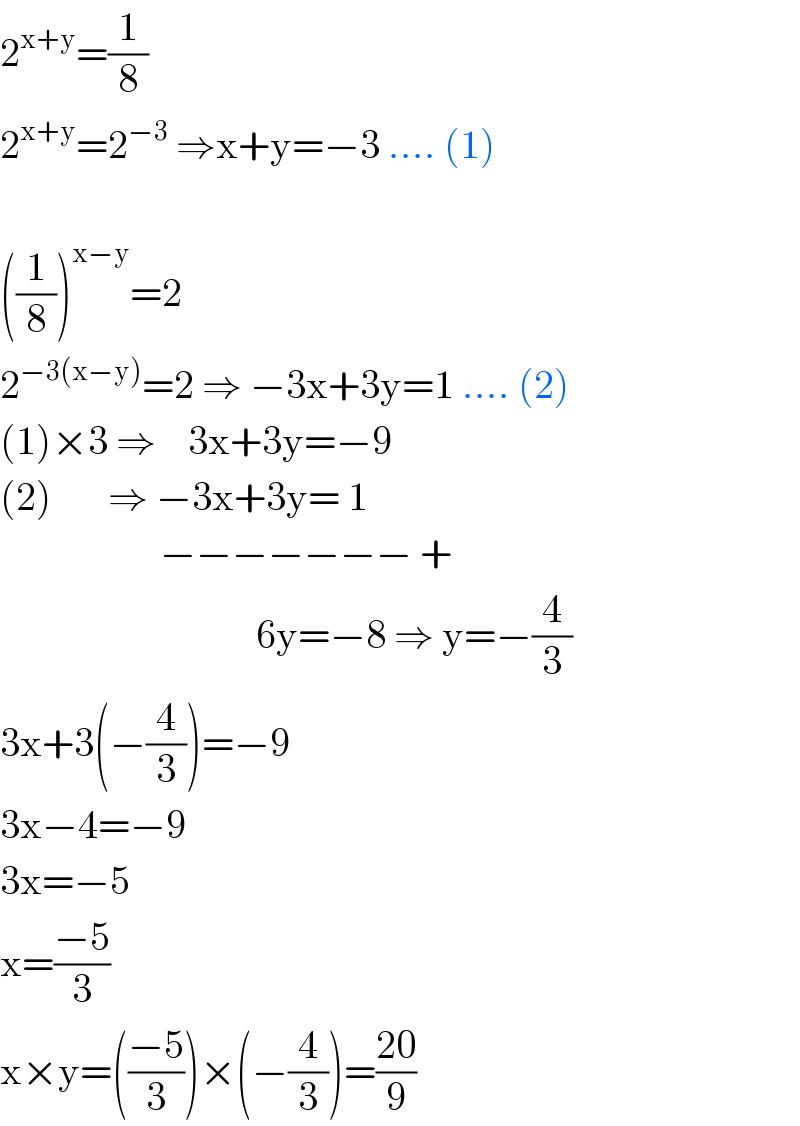
$$\mathrm{2}^{\mathrm{x}+\mathrm{y}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{2}^{\mathrm{x}+\mathrm{y}} =\mathrm{2}^{−\mathrm{3}} \:\Rightarrow\mathrm{x}+\mathrm{y}=−\mathrm{3}\:....\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{x}−\mathrm{y}} =\mathrm{2} \\ $$$$\mathrm{2}^{−\mathrm{3}\left(\mathrm{x}−\mathrm{y}\right)} =\mathrm{2}\:\Rightarrow\:−\mathrm{3x}+\mathrm{3y}=\mathrm{1}\:....\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)×\mathrm{3}\:\Rightarrow\:\:\:\:\mathrm{3x}+\mathrm{3y}=−\mathrm{9} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\Rightarrow\:−\mathrm{3x}+\mathrm{3y}=\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−\:+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6y}=−\mathrm{8}\:\Rightarrow\:\mathrm{y}=−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{3x}+\mathrm{3}\left(−\frac{\mathrm{4}}{\mathrm{3}}\right)=−\mathrm{9} \\ $$$$\mathrm{3x}−\mathrm{4}=−\mathrm{9} \\ $$$$\mathrm{3x}=−\mathrm{5} \\ $$$$\mathrm{x}=\frac{−\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{x}×\mathrm{y}=\left(\frac{−\mathrm{5}}{\mathrm{3}}\right)×\left(−\frac{\mathrm{4}}{\mathrm{3}}\right)=\frac{\mathrm{20}}{\mathrm{9}} \\ $$
