
Question Number 101330 by 175 last updated on 01/Jul/20
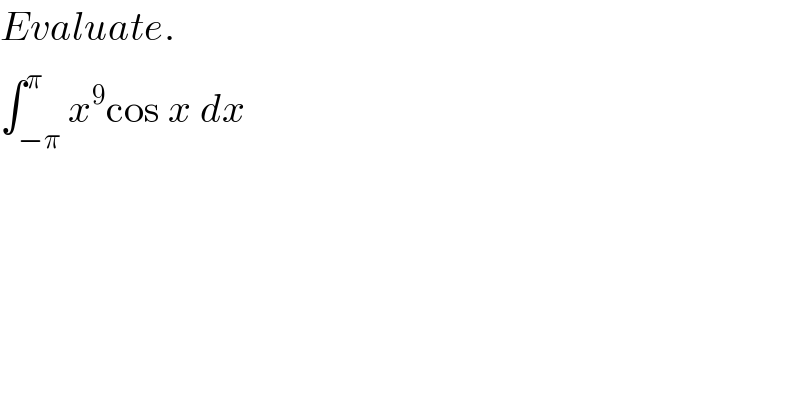
$${Evaluate}. \\ $$$$\int_{−\pi} ^{\pi} {x}^{\mathrm{9}} \mathrm{cos}\:{x}\:{dx} \\ $$
Commented by mr W last updated on 01/Jul/20
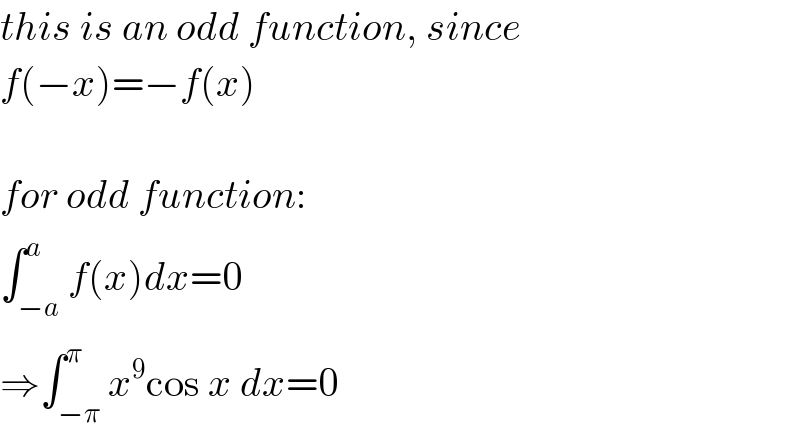
$${this}\:{is}\:{an}\:{odd}\:{function},\:{since} \\ $$$${f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$$$ \\ $$$${for}\:{odd}\:{function}: \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}=\mathrm{0} \\ $$$$\Rightarrow\int_{−\pi} ^{\pi} {x}^{\mathrm{9}} \mathrm{cos}\:{x}\:{dx}=\mathrm{0} \\ $$
Commented by ajfour last updated on 02/Jul/20
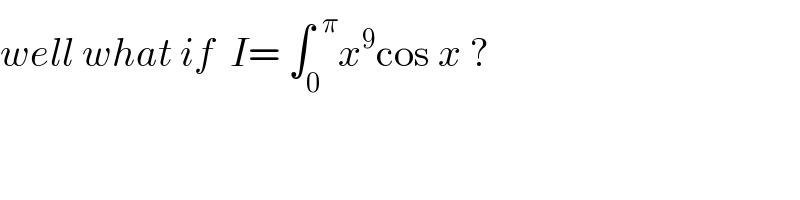
$${well}\:{what}\:{if}\:\:{I}=\:\int_{\mathrm{0}} ^{\:\:\pi} {x}^{\mathrm{9}} \mathrm{cos}\:{x}\:? \\ $$
Commented by mr W last updated on 02/Jul/20
![I_(2n+1) =−(2n+1)[π^(2n) +(2n)I_(2n−1) ] ....](Q101385.png)
$${I}_{\mathrm{2}{n}+\mathrm{1}} =−\left(\mathrm{2}{n}+\mathrm{1}\right)\left[\pi^{\mathrm{2}{n}} +\left(\mathrm{2}{n}\right){I}_{\mathrm{2}{n}−\mathrm{1}} \right] \\ $$$$.... \\ $$
Commented by ajfour last updated on 02/Jul/20

$${thanks}\:{Sir}! \\ $$
Commented by 1549442205 last updated on 02/Jul/20
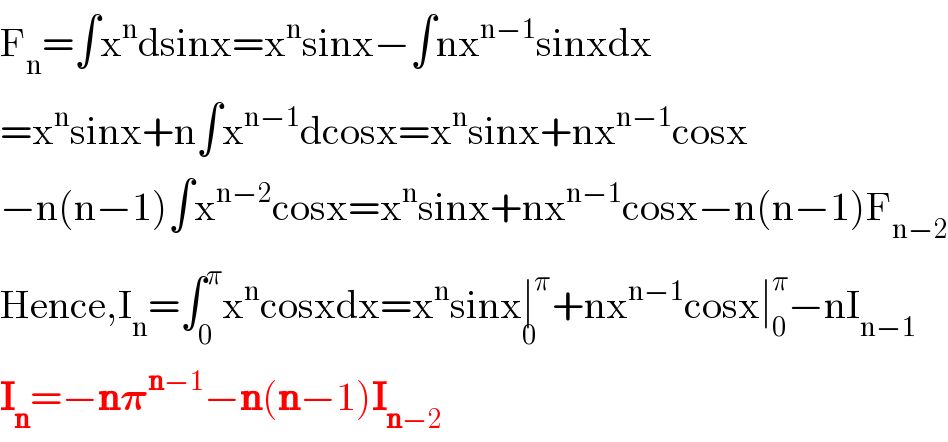
$$\mathrm{F}_{\mathrm{n}} =\int\mathrm{x}^{\mathrm{n}} \mathrm{dsinx}=\mathrm{x}^{\mathrm{n}} \mathrm{sinx}−\int\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \mathrm{sinxdx} \\ $$$$=\mathrm{x}^{\mathrm{n}} \mathrm{sinx}+\mathrm{n}\int\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{dcosx}=\mathrm{x}^{\mathrm{n}} \mathrm{sinx}+\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \mathrm{cosx} \\ $$$$−\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\int\mathrm{x}^{\mathrm{n}−\mathrm{2}} \mathrm{cosx}=\mathrm{x}^{\mathrm{n}} \mathrm{sinx}+\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \mathrm{cosx}−\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{F}_{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{Hence},\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\pi} \mathrm{x}^{\mathrm{n}} \mathrm{cosxdx}=\mathrm{x}^{\mathrm{n}} \mathrm{sinx}\underset{\mathrm{0}} {\mid}^{\pi} +\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \mathrm{cosx}\mid_{\mathrm{0}} ^{\pi} −\mathrm{nI}_{\mathrm{n}−\mathrm{1}} \\ $$$$\boldsymbol{\mathrm{I}}_{\boldsymbol{\mathrm{n}}} =−\boldsymbol{\mathrm{n}\pi}^{\boldsymbol{\mathrm{n}}−\mathrm{1}} −\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\boldsymbol{\mathrm{I}}_{\boldsymbol{\mathrm{n}}−\mathrm{2}} \\ $$
