
Question Number 101291 by Mikael_786 last updated on 01/Jul/20

Answered by mr W last updated on 01/Jul/20
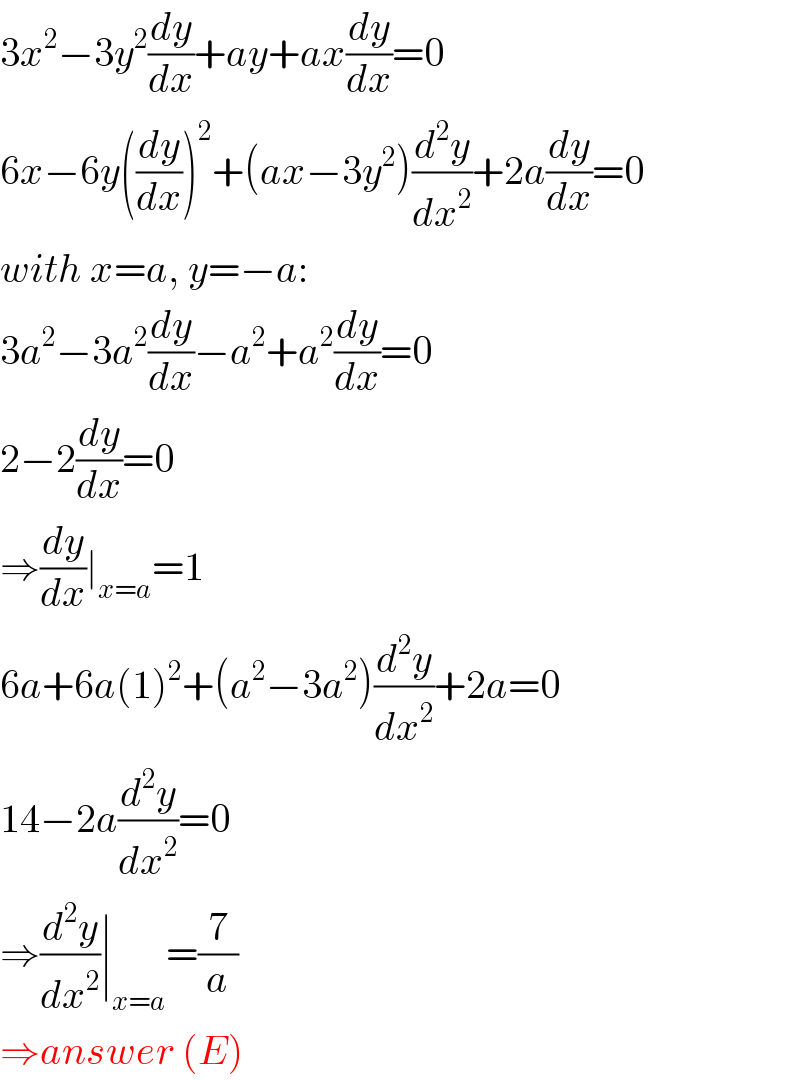
$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} \frac{{dy}}{{dx}}+{ay}+{ax}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{6}{x}−\mathrm{6}{y}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} +\left({ax}−\mathrm{3}{y}^{\mathrm{2}} \right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{2}{a}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${with}\:{x}={a},\:{y}=−{a}: \\ $$$$\mathrm{3}{a}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \frac{{dy}}{{dx}}−{a}^{\mathrm{2}} +{a}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{2}−\mathrm{2}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}\mid_{{x}={a}} =\mathrm{1} \\ $$$$\mathrm{6}{a}+\mathrm{6}{a}\left(\mathrm{1}\right)^{\mathrm{2}} +\left({a}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{2}{a}=\mathrm{0} \\ $$$$\mathrm{14}−\mathrm{2}{a}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\mid_{{x}={a}} =\frac{\mathrm{7}}{{a}} \\ $$$$\Rightarrow{answer}\:\left({E}\right) \\ $$
Commented by Mikael_786 last updated on 02/Jul/20

$${thank}\:{you} \\ $$
