
Question Number 101225 by harckinwunmy last updated on 01/Jul/20
Commented by Dwaipayan Shikari last updated on 01/Jul/20
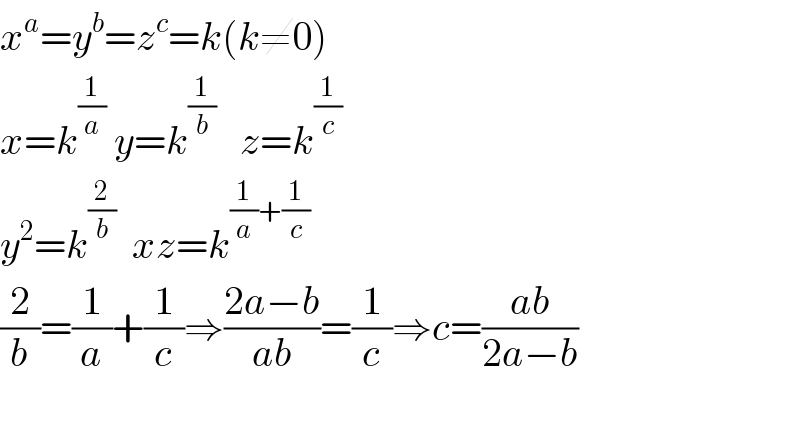
$${x}^{{a}} ={y}^{{b}} ={z}^{{c}} ={k}\left({k}\neq\mathrm{0}\right) \\ $$$${x}={k}^{\frac{\mathrm{1}}{{a}}} \:{y}={k}^{\frac{\mathrm{1}}{{b}}} \:\:\:{z}={k}^{\frac{\mathrm{1}}{{c}}} \\ $$$${y}^{\mathrm{2}} ={k}^{\frac{\mathrm{2}}{{b}}} \:\:{xz}={k}^{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{c}}} \\ $$$$\frac{\mathrm{2}}{{b}}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{c}}\Rightarrow\frac{\mathrm{2}{a}−{b}}{{ab}}=\frac{\mathrm{1}}{{c}}\Rightarrow{c}=\frac{{ab}}{\mathrm{2}{a}−{b}} \\ $$$$ \\ $$
Commented by smridha last updated on 01/Jul/20
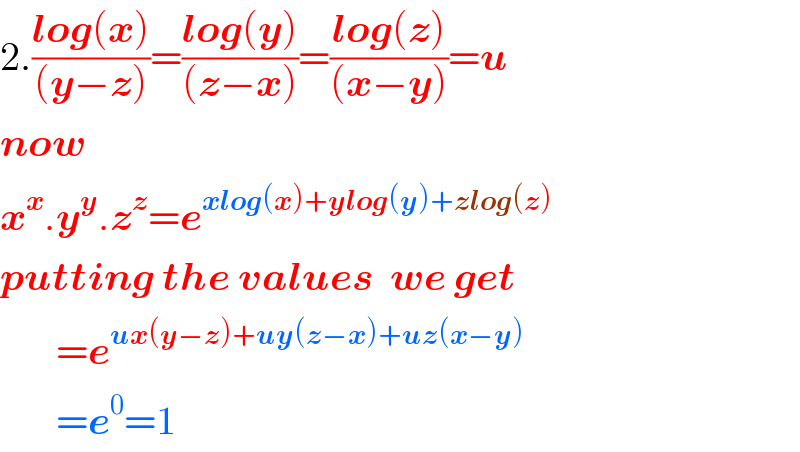
$$\mathrm{2}.\frac{\boldsymbol{{log}}\left(\boldsymbol{{x}}\right)}{\left(\boldsymbol{{y}}−\boldsymbol{{z}}\right)}=\frac{\boldsymbol{{log}}\left(\boldsymbol{{y}}\right)}{\left(\boldsymbol{{z}}−\boldsymbol{{x}}\right)}=\frac{\boldsymbol{{log}}\left(\boldsymbol{{z}}\right)}{\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right)}=\boldsymbol{{u}} \\ $$$$\boldsymbol{{now}}\: \\ $$$$\boldsymbol{{x}}^{\boldsymbol{{x}}} .\boldsymbol{{y}}^{\boldsymbol{{y}}} .\boldsymbol{{z}}^{\boldsymbol{{z}}} =\boldsymbol{{e}}^{\boldsymbol{{xlog}}\left(\boldsymbol{{x}}\right)+\boldsymbol{{ylog}}\left(\boldsymbol{{y}}\right)+\boldsymbol{{zlog}}\left(\boldsymbol{{z}}\right)} \\ $$$$\boldsymbol{{putting}}\:\boldsymbol{{the}}\:\boldsymbol{{values}}\:\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\:\:\:\:\:\:\:=\boldsymbol{{e}}^{\boldsymbol{{ux}}\left(\boldsymbol{{y}}−\boldsymbol{{z}}\right)+\boldsymbol{{uy}}\left(\boldsymbol{{z}}−\boldsymbol{{x}}\right)+\boldsymbol{{uz}}\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right)} \\ $$$$\:\:\:\:\:\:\:=\boldsymbol{{e}}^{\mathrm{0}} =\mathrm{1} \\ $$
Commented by bemath last updated on 01/Jul/20
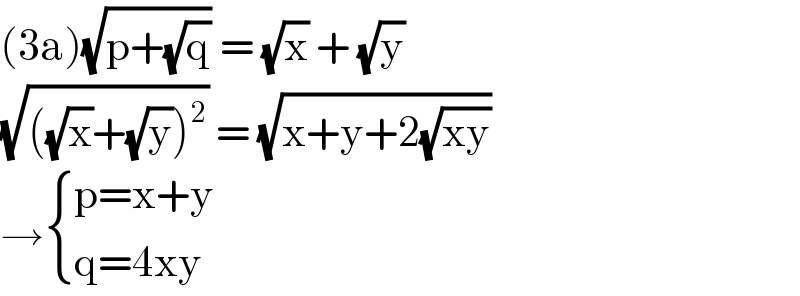
$$\left(\mathrm{3a}\right)\sqrt{\mathrm{p}+\sqrt{\mathrm{q}}}\:=\:\sqrt{\mathrm{x}}\:+\:\sqrt{\mathrm{y}} \\ $$$$\sqrt{\left(\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}\right)^{\mathrm{2}} }\:=\:\sqrt{\mathrm{x}+\mathrm{y}+\mathrm{2}\sqrt{\mathrm{xy}}} \\ $$$$\rightarrow\begin{cases}{\mathrm{p}=\mathrm{x}+\mathrm{y}}\\{\mathrm{q}=\mathrm{4xy}}\end{cases}\: \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
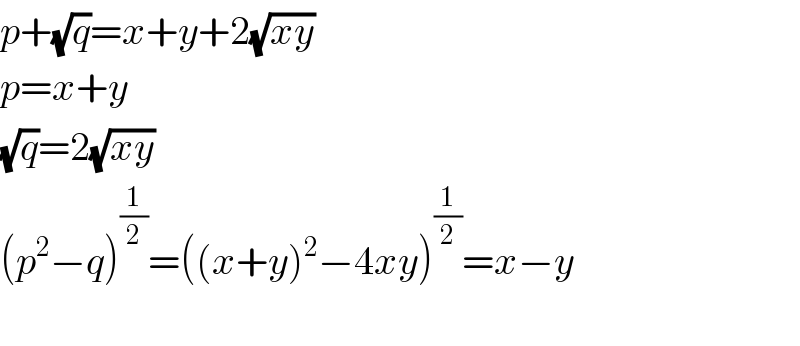
$${p}+\sqrt{{q}}={x}+{y}+\mathrm{2}\sqrt{{xy}} \\ $$$${p}={x}+{y} \\ $$$$\sqrt{{q}}=\mathrm{2}\sqrt{{xy}} \\ $$$$\left({p}^{\mathrm{2}} −{q}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={x}−{y} \\ $$$$ \\ $$
