
Question Number 101183 by PengagumRahasiamu last updated on 01/Jul/20

Answered by $@y@m last updated on 01/Jul/20
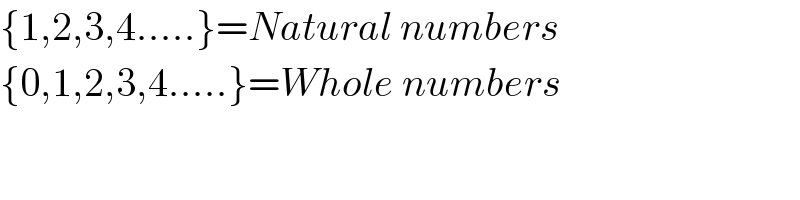
$$\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}.....\right\}={Natural}\:{numbers} \\ $$$$\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}.....\right\}={Whole}\:{numbers} \\ $$
Commented by 1549442205 last updated on 01/Jul/20

$$\mathrm{As}\:\mathrm{I}\:\mathrm{known}\:,\mathrm{by}\:\mathrm{new}\:\mathrm{definition}\:\mathrm{set}\:\mathrm{of}\:\mathrm{natural}\: \\ $$$$\mathrm{numbers}\:\mathrm{insists}\:\mathrm{of}\:\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},...\right\}\mathrm{and}\: \\ $$$$\mathrm{is}\:\mathrm{denoted}\:\mathrm{by}\:\mathrm{symbol}\:\mathbb{N},\mathrm{the}\:\mathrm{set}\:\mathrm{of} \\ $$$$\mathrm{numbers}\:\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\}\:\mathrm{is}\:\mathrm{denoted}\:\mathrm{by}\:\mathbb{N}^{\ast} \\ $$$$\mathbb{N}^{\ast} =\mathbb{N}−\left\{\mathrm{0}\right\} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jul/20

$${In}\:{some}\:{books}\:{however}\:{the}\:{set} \\ $$$$\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}.....\right\}\:{is}\:{referred}\:{as} \\ $$$${Natural}\:{numbers}. \\ $$
Commented by $@y@m last updated on 01/Jul/20

$${Agree}. \\ $$
Commented by MJS last updated on 01/Jul/20
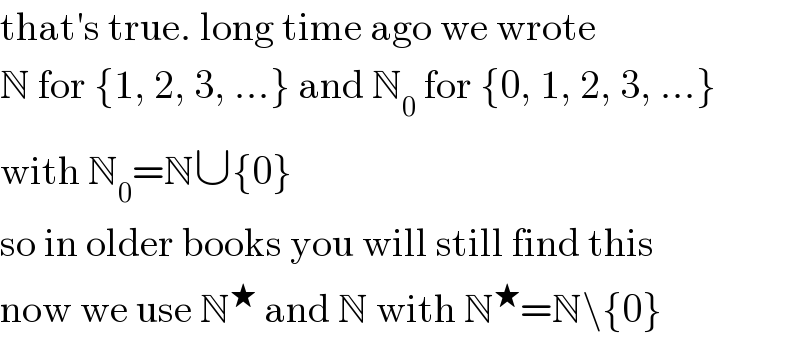
$$\mathrm{that}'\mathrm{s}\:\mathrm{true}.\:\mathrm{long}\:\mathrm{time}\:\mathrm{ago}\:\mathrm{we}\:\mathrm{wrote} \\ $$$$\mathbb{N}\:\mathrm{for}\:\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\right\}\:\mathrm{and}\:\mathbb{N}_{\mathrm{0}} \:\mathrm{for}\:\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\right\} \\ $$$$\mathrm{with}\:\mathbb{N}_{\mathrm{0}} =\mathbb{N}\cup\left\{\mathrm{0}\right\} \\ $$$$\mathrm{so}\:\mathrm{in}\:\mathrm{older}\:\mathrm{books}\:\mathrm{you}\:\mathrm{will}\:\mathrm{still}\:\mathrm{find}\:\mathrm{this} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{use}\:\mathbb{N}^{\bigstar} \:\mathrm{and}\:\mathbb{N}\:\mathrm{with}\:\mathbb{N}^{\bigstar} =\mathbb{N}\backslash\left\{\mathrm{0}\right\} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jul/20

$${First}\:{numbers}\:{ever}\:{used}\:{by}\:{humans} \\ $$$${were}\:\mathrm{1},\mathrm{2},\mathrm{3},...\:{So}\:{in}\:{a}\:{sense}\:{these}\:{are} \\ $$$$'{natural}'.\: \\ $$
