
Question Number 101116 by Jamshidbek2311 last updated on 30/Jun/20
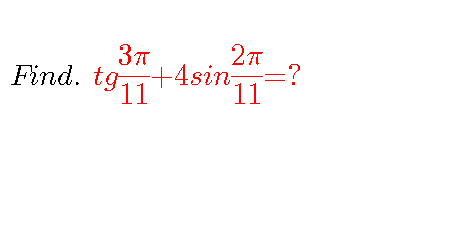
Answered by 1549442205 last updated on 07/Jul/20
![We prove that tan((3𝛑)/(11))+4sin ((2𝛑)/(11))=(√(11)) ⇔sin((3π)/(11))+4sin((2π)/(11))cos((3π)/(11))=(√(11))cos((3π)/(11)) ⇔3sin(π/(11))−4sin^3 (π/(11))+4(2sin(π/(11))cos(π/(11))− (√(11)) )( 4cos^3 (π/(11))−3cos(π/(11)))=0 ⇔sin(π/(11))[3−4(1−cos^2 (π/(11)))]+4(2sin(π/(11))cos(π/(11))− (√(11)) )( 4cos^3 (π/(11))−3cos(π/(11)))=0 ⇔sin(π/(11))(4cos^2 (π/(11))−1)+4(2sin(π/(11))cos(π/(11))− (√(11)) )( 4cos^3 (π/(11))−3cos(π/(11)))=0 Putting cos(π/(11))=x ⇒sin(π/(11))=(√(1−x^2 )) we get (√(1−x^2 ))(4x^2 −1)+4(2x(√(1−x^2 ))−(√(11)))(4x^3 −3x)=0 ⇔(√(1−x^2 ))(32x^4 −20x^2 −1)=(√(11))(4x^3 −3x) Square two sides of above we get (1−x^2 )(1024x^8 −1280x^6 +336x^4 +40x^2 +1)=11(16x^6 −24x^4 +9x^2 ) ⇔(−1024x^(10) +2304x^8 −1616x^6 +296x^4 +39x^2 +1=176x^6 −264x^4 +99x^2 ⇔1024x^(10) −2304x^8 +1792x^6 −560x^4 +60x^2 −1=0 =(32x^5 −16x^4 −32x^3 +12x^2 +6x−1)(32x^5 +16x^4 −32x^3 −12x^2 +6x+1)=0 ⇔(32x^5 −16x^4 −32x^3 +12x^2 +6x−1)=0 (∗) (because (32x^5 +16x^4 −32x^3 −12x^2 +6x+1≠0 for x=(π/(11))) Now we need prove the equality is true. Indeed, Applying Mauvra′s formular we have (cos(π/(11))+isin(π/(11)))^5 =cos((5π)/(11))+isin((5π)/(11)) ⇔cos^5 (π/(11))+5icos^4 (π/(11))sin(π/(11))+10i^2 cos^3 (π/(11))sin^2 (π/(11))+10cos^2 .i^3 sin^3 (π/(11))+5cos(π/(11)).i^4 sin^4 (π/(11))+sin^5 (π/(11))=cos((5π)/(11))+isin((5π)/(11)) ⇒cos((5𝛑)/(11))=cos^5 (π/(11))−10cos^3 (π/(11))sin^2 (π/(11))+5cos(π/(11))sin^4 (π/(11)) =cos^5 (π/(11))−10cos^3 (π/(11))(1−cos^2 (π/(11)))+5cos(π/(11))(1−cos^2 (π/(11)))^2 =16cos^5 (𝛑/(11))−20cos^3 (𝛑/(11))+5cos(𝛑/(11))(1) (cos(π/(11))+isin(π/(11)))^6 =cos((6π)/(11))+isin((6π)/(11))=−cos((5π)/(11))+isin((5π)/(11)) cos^6 (π/(11))+6cos^5 (π/(11)).isin(π/(11))+15cos^4 (π/(11)).i^2 sin^2 (π/(11))+20cos^3 (π/(11)).i^3 sin^3 (π/(11))+15cos^2 (π/(11)).i^4 sin^4 (π/(11)) +5cos(π/(11)).i^5 sin^5 (π/(11))+sin^6 (π/(11))=−cos((5π)/(11))+isin((5π)/(11)) ⇔x^6 −15x^4 y^2 +15x^2 y^4 +y^6 +i.(6x^5 y−15x^4 y^2 −20x^3 y^3 )=−cos((5𝛑)/(11))+isin((5𝛑)/(11))(y=sin(𝛑/(11)))(2) From (1) (2) we get x^6 −15x^4 y^2 +15x^2 y^4 +y^6 =−16x^5 +20x^3 −5x ⇔x^6 −15x^4 (1−x^2 )+15x^2 (1−x^2 )^2 +(1−x^2 )^3 =−16x^5 +20x^3 −5x ⇔32x^6 −48x^4 +18x^2 −1=−16x^5 +20x^3 −5x ⇔32x^6 +16x^6 −48x^4 −20x^3 +18x^2 +5x−1=0 ⇔(x+1)(16x^5 −16x^4 −32x^3 +12x^2 +6x−1)=0 ⇔16x^5 −16x^4 −32x^3 +12x^2 +6x−1=0 Thus,the equality (∗)proved Therefore,tan((3𝛑)/(11))+4sin((2𝛑)/(11))=(√(11 )) (q.e.d)](Q102045.png)
$$\boldsymbol{\mathrm{We}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{tan}}\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{11}}+\mathrm{4}\boldsymbol{\mathrm{sin}}\:\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{11}}=\sqrt{\mathrm{11}} \\ $$$$\Leftrightarrow\mathrm{sin}\frac{\mathrm{3}\pi}{\mathrm{11}}+\mathrm{4sin}\frac{\mathrm{2}\pi}{\mathrm{11}}\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{11}}=\sqrt{\mathrm{11}}\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{11}} \\ $$$$\Leftrightarrow\mathrm{3sin}\frac{\pi}{\mathrm{11}}−\mathrm{4sin}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}+\mathrm{4}\left(\mathrm{2sin}\frac{\pi}{\mathrm{11}}\mathrm{cos}\frac{\pi}{\mathrm{11}}−\:\sqrt{\mathrm{11}}\:\right)\left(\:\mathrm{4cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}−\mathrm{3cos}\frac{\pi}{\mathrm{11}}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{sin}\frac{\pi}{\mathrm{11}}\left[\mathrm{3}−\mathrm{4}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}\right)\right]+\mathrm{4}\left(\mathrm{2sin}\frac{\pi}{\mathrm{11}}\mathrm{cos}\frac{\pi}{\mathrm{11}}−\:\sqrt{\mathrm{11}}\:\right)\left(\:\mathrm{4cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}−\mathrm{3cos}\frac{\pi}{\mathrm{11}}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{sin}\frac{\pi}{\mathrm{11}}\left(\mathrm{4cos}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}−\mathrm{1}\right)+\mathrm{4}\left(\mathrm{2sin}\frac{\pi}{\mathrm{11}}\mathrm{cos}\frac{\pi}{\mathrm{11}}−\:\sqrt{\mathrm{11}}\:\right)\left(\:\mathrm{4cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}−\mathrm{3cos}\frac{\pi}{\mathrm{11}}\right)=\mathrm{0} \\ $$$$\mathrm{Putting}\:\:\:\mathrm{cos}\frac{\pi}{\mathrm{11}}=\mathrm{x}\:\Rightarrow\mathrm{sin}\frac{\pi}{\mathrm{11}}=\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{get} \\ $$$$\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\left(\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{4}\left(\mathrm{2}\boldsymbol{\mathrm{x}}\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }−\sqrt{\mathrm{11}}\right)\left(\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\left(\mathrm{32x}^{\mathrm{4}} −\mathrm{20x}^{\mathrm{2}} −\mathrm{1}\right)=\sqrt{\mathrm{11}}\left(\mathrm{4x}^{\mathrm{3}} −\mathrm{3x}\right) \\ $$$$\mathrm{Square}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{above}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1024x}^{\mathrm{8}} −\mathrm{1280x}^{\mathrm{6}} +\mathrm{336x}^{\mathrm{4}} +\mathrm{40x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{11}\left(\mathrm{16x}^{\mathrm{6}} −\mathrm{24x}^{\mathrm{4}} +\mathrm{9x}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\left(−\mathrm{1024x}^{\mathrm{10}} +\mathrm{2304x}^{\mathrm{8}} −\mathrm{1616x}^{\mathrm{6}} +\mathrm{296x}^{\mathrm{4}} +\mathrm{39x}^{\mathrm{2}} +\mathrm{1}=\mathrm{176x}^{\mathrm{6}} −\mathrm{264x}^{\mathrm{4}} +\mathrm{99x}^{\mathrm{2}} \right. \\ $$$$\Leftrightarrow\mathrm{1024x}^{\mathrm{10}} −\mathrm{2304x}^{\mathrm{8}} +\mathrm{1792x}^{\mathrm{6}} −\mathrm{560x}^{\mathrm{4}} +\mathrm{60x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$=\left(\mathrm{32x}^{\mathrm{5}} −\mathrm{16x}^{\mathrm{4}} −\mathrm{32x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{1}\right)\left(\mathrm{32x}^{\mathrm{5}} +\mathrm{16x}^{\mathrm{4}} −\mathrm{32x}^{\mathrm{3}} −\mathrm{12x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{32}\boldsymbol{\mathrm{x}}^{\mathrm{5}} −\mathrm{16}\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\mathrm{32}\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{12}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{\mathrm{x}}−\mathrm{1}\right)=\mathrm{0}\:\left(\ast\right) \\ $$$$\left(\mathrm{because}\:\left(\mathrm{32x}^{\mathrm{5}} +\mathrm{16x}^{\mathrm{4}} −\mathrm{32x}^{\mathrm{3}} −\mathrm{12x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{1}\neq\mathrm{0}\:\mathrm{for}\:\mathrm{x}=\frac{\pi}{\mathrm{11}}\right)\right. \\ $$$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equality}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{true}}. \\ $$$$\boldsymbol{\mathrm{Indeed}}, \\ $$$$\mathrm{Applying}\:\mathrm{Mauvra}'\mathrm{s}\:\mathrm{formular}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{cos}\frac{\pi}{\mathrm{11}}+\mathrm{isin}\frac{\pi}{\mathrm{11}}\right)^{\mathrm{5}} =\mathrm{cos}\frac{\mathrm{5}\pi}{\mathrm{11}}+\mathrm{isin}\frac{\mathrm{5}\pi}{\mathrm{11}} \\ $$$$\Leftrightarrow\mathrm{cos}^{\mathrm{5}} \frac{\pi}{\mathrm{11}}+\mathrm{5icos}^{\mathrm{4}} \frac{\pi}{\mathrm{11}}\mathrm{sin}\frac{\pi}{\mathrm{11}}+\mathrm{10i}^{\mathrm{2}} \mathrm{cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}+\mathrm{10cos}^{\mathrm{2}} .\mathrm{i}^{\mathrm{3}} \mathrm{sin}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}+\mathrm{5cos}\frac{\pi}{\mathrm{11}}.\mathrm{i}^{\mathrm{4}} \mathrm{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{11}}+\mathrm{sin}^{\mathrm{5}} \frac{\pi}{\mathrm{11}}=\mathrm{cos}\frac{\mathrm{5}\pi}{\mathrm{11}}+\mathrm{isin}\frac{\mathrm{5}\pi}{\mathrm{11}} \\ $$$$\:\Rightarrow\boldsymbol{\mathrm{cos}}\frac{\mathrm{5}\boldsymbol{\pi}}{\mathrm{11}}=\mathrm{cos}^{\mathrm{5}} \frac{\pi}{\mathrm{11}}−\mathrm{10cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}+\mathrm{5cos}\frac{\pi}{\mathrm{11}}\mathrm{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{11}} \\ $$$$=\mathrm{cos}^{\mathrm{5}} \frac{\pi}{\mathrm{11}}−\mathrm{10cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}\right)+\mathrm{5cos}\frac{\pi}{\mathrm{11}}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{16}\boldsymbol{\mathrm{cos}}^{\mathrm{5}} \frac{\boldsymbol{\pi}}{\mathrm{11}}−\mathrm{20}\boldsymbol{\mathrm{cos}}^{\mathrm{3}} \frac{\boldsymbol{\pi}}{\mathrm{11}}+\mathrm{5}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\pi}}{\mathrm{11}}\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{cos}\frac{\pi}{\mathrm{11}}+\mathrm{isin}\frac{\pi}{\mathrm{11}}\right)^{\mathrm{6}} =\mathrm{cos}\frac{\mathrm{6}\pi}{\mathrm{11}}+\mathrm{isin}\frac{\mathrm{6}\pi}{\mathrm{11}}=−\mathrm{cos}\frac{\mathrm{5}\pi}{\mathrm{11}}+\mathrm{isin}\frac{\mathrm{5}\pi}{\mathrm{11}} \\ $$$$\mathrm{cos}^{\mathrm{6}} \frac{\pi}{\mathrm{11}}+\mathrm{6cos}^{\mathrm{5}} \frac{\pi}{\mathrm{11}}.\mathrm{isin}\frac{\pi}{\mathrm{11}}+\mathrm{15cos}^{\mathrm{4}} \frac{\pi}{\mathrm{11}}.\mathrm{i}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}+\mathrm{20cos}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}.\mathrm{i}^{\mathrm{3}} \mathrm{sin}^{\mathrm{3}} \frac{\pi}{\mathrm{11}}+\mathrm{15cos}^{\mathrm{2}} \frac{\pi}{\mathrm{11}}.\mathrm{i}^{\mathrm{4}} \mathrm{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{11}} \\ $$$$+\mathrm{5cos}\frac{\pi}{\mathrm{11}}.\mathrm{i}^{\mathrm{5}} \mathrm{sin}^{\mathrm{5}} \frac{\pi}{\mathrm{11}}+\mathrm{sin}^{\mathrm{6}} \frac{\pi}{\mathrm{11}}=−\mathrm{cos}\frac{\mathrm{5}\pi}{\mathrm{11}}+\mathrm{isin}\frac{\mathrm{5}\pi}{\mathrm{11}} \\ $$$$\Leftrightarrow\boldsymbol{\mathrm{x}}^{\mathrm{6}} −\mathrm{15}\boldsymbol{\mathrm{x}}^{\mathrm{4}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{15}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{4}} +\boldsymbol{\mathrm{y}}^{\mathrm{6}} +\boldsymbol{\mathrm{i}}.\left(\mathrm{6}\boldsymbol{\mathrm{x}}^{\mathrm{5}} \boldsymbol{\mathrm{y}}−\mathrm{15}\boldsymbol{\mathrm{x}}^{\mathrm{4}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{20}\boldsymbol{\mathrm{x}}^{\mathrm{3}} \boldsymbol{\mathrm{y}}^{\mathrm{3}} \right)=−\boldsymbol{\mathrm{cos}}\frac{\mathrm{5}\boldsymbol{\pi}}{\mathrm{11}}+\boldsymbol{\mathrm{isin}}\frac{\mathrm{5}\boldsymbol{\pi}}{\mathrm{11}}\left(\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\pi}}{\mathrm{11}}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}^{\mathrm{6}} −\mathrm{15x}^{\mathrm{4}} \mathrm{y}^{\mathrm{2}} +\mathrm{15x}^{\mathrm{2}} \mathrm{y}^{\mathrm{4}} +\mathrm{y}^{\mathrm{6}} =−\mathrm{16x}^{\mathrm{5}} +\mathrm{20x}^{\mathrm{3}} −\mathrm{5x} \\ $$$$\:\Leftrightarrow\mathrm{x}^{\mathrm{6}} −\mathrm{15x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{15x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} =−\mathrm{16x}^{\mathrm{5}} +\mathrm{20x}^{\mathrm{3}} −\mathrm{5x} \\ $$$$\Leftrightarrow\mathrm{32x}^{\mathrm{6}} −\mathrm{48x}^{\mathrm{4}} +\mathrm{18x}^{\mathrm{2}} −\mathrm{1}=−\mathrm{16x}^{\mathrm{5}} +\mathrm{20x}^{\mathrm{3}} −\mathrm{5x} \\ $$$$\Leftrightarrow\mathrm{32x}^{\mathrm{6}} +\mathrm{16x}^{\mathrm{6}} −\mathrm{48x}^{\mathrm{4}} −\mathrm{20x}^{\mathrm{3}} +\mathrm{18x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{16x}^{\mathrm{5}} −\mathrm{16x}^{\mathrm{4}} −\mathrm{32x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{16}\boldsymbol{\mathrm{x}}^{\mathrm{5}} −\mathrm{16}\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\mathrm{32}\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{12}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{\mathrm{x}}−\mathrm{1}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equality}}\:\left(\ast\right)\boldsymbol{\mathrm{proved}}\: \\ $$$$\boldsymbol{\mathrm{Therefore}},\boldsymbol{\mathrm{tan}}\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{11}}+\mathrm{4}\boldsymbol{\mathrm{sin}}\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{11}}=\sqrt{\mathrm{11}\:}\:\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$
