
Question Number 101082 by 67549972 last updated on 30/Jun/20
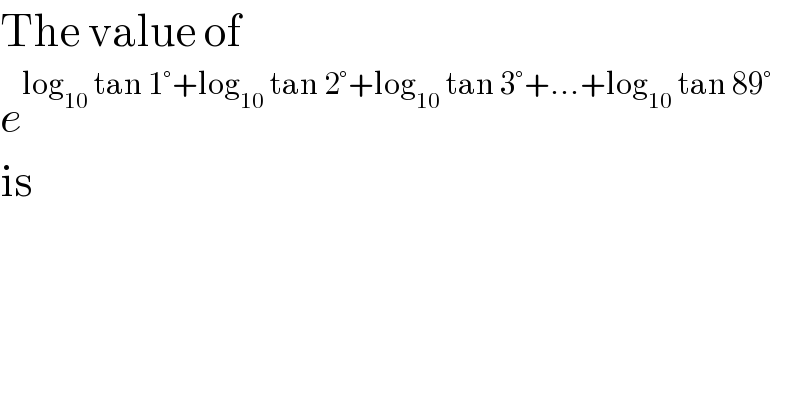
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of} \\ $$$${e}^{\mathrm{log}_{\mathrm{10}} \:\mathrm{tan}\:\mathrm{1}°+\mathrm{log}_{\mathrm{10}} \:\mathrm{tan}\:\mathrm{2}°+\mathrm{log}_{\mathrm{10}} \:\mathrm{tan}\:\mathrm{3}°+...+\mathrm{log}_{\mathrm{10}} \:\mathrm{tan}\:\mathrm{89}°} \\ $$$$\mathrm{is} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Jun/20
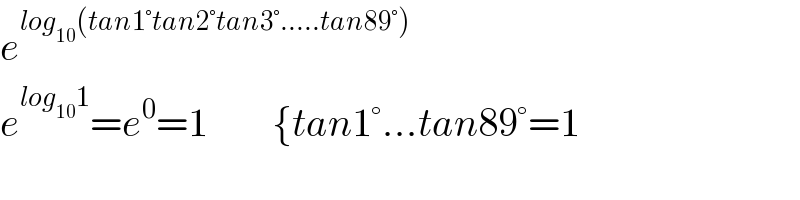
$${e}^{{log}_{\mathrm{10}} \left({tan}\mathrm{1}°{tan}\mathrm{2}°{tan}\mathrm{3}°.....{tan}\mathrm{89}°\right)} \\ $$$${e}^{{log}_{\mathrm{10}} \mathrm{1}} ={e}^{\mathrm{0}} =\mathrm{1}\:\:\:\:\:\:\:\:\left\{{tan}\mathrm{1}°...{tan}\mathrm{89}°=\mathrm{1}\right. \\ $$
Commented by smridha last updated on 01/Jul/20
![e^(log_(10) [tan1^° .tan2^° .tan3^° ...tan89^° ]) =e^(log_(10) [tan1^° .tan2^° .tan3°...cot3^° .cot2^° .cot1^° ]) =e^(log_(10) 1) =e^0 =1.](Q101087.png)
$$\boldsymbol{{e}}^{\boldsymbol{{log}}_{\mathrm{10}} \left[\boldsymbol{{tan}}\mathrm{1}^{°} .\boldsymbol{{tan}}\mathrm{2}^{°} .\boldsymbol{{tan}}\mathrm{3}^{°} ...{tan}\mathrm{89}^{°} \right]} \\ $$$$=\boldsymbol{{e}}^{\boldsymbol{{log}}_{\mathrm{10}} \left[\boldsymbol{{tan}}\mathrm{1}^{°} .\boldsymbol{{tan}}\mathrm{2}^{°} .\boldsymbol{{tan}}\mathrm{3}°...\boldsymbol{{cot}}\mathrm{3}^{°} .\boldsymbol{{cot}}\mathrm{2}^{°} .\boldsymbol{{cot}}\mathrm{1}^{°} \right]} \\ $$$$={e}^{\boldsymbol{{log}}_{\mathrm{10}} \mathrm{1}} =\boldsymbol{{e}}^{\mathrm{0}} =\mathrm{1}. \\ $$
