
Question Number 101057 by bemath last updated on 30/Jun/20
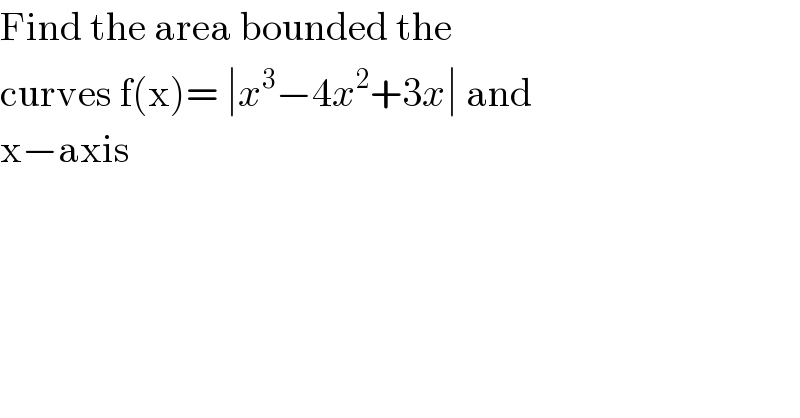
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{bounded}\:\mathrm{the}\: \\ $$$$\mathrm{curves}\:\mathrm{f}\left(\mathrm{x}\right)=\:\mid{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}\mid\:\mathrm{and}\: \\ $$$$\mathrm{x}−\mathrm{axis}\: \\ $$
Answered by john santu last updated on 30/Jun/20
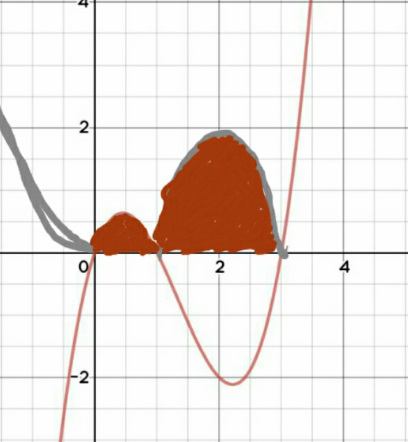
Commented by john santu last updated on 30/Jun/20
![Area = ∫_0 ^1 (x^3 −4x^2 +3x) dx −∫_1 ^3 (x^3 −4x^2 +3x)dx = [(1/4)x^4 −(4/3)x^3 +(3/2)x^2 ]_0 ^1 − [ (1/4)x^4 −(4/3)x^3 +(3/2)x^2 ]_1 ^3 = (5/(12))−((1/4)(80)−(4/3)(26)+(3/2)(8)) = (5/(12))+((104)/3)−32 = (5/(12)) + (8/3) = ((37)/(12))★](Q101059.png)
$$\mathrm{Area}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}\right)\:{dx}\:−\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\left({x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}\right){dx} \\ $$$$=\:\left[\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} − \\ $$$$\left[\:\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}} \: \\ $$$$=\:\frac{\mathrm{5}}{\mathrm{12}}−\left(\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{80}\right)−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{26}\right)+\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{8}\right)\right) \\ $$$$=\:\frac{\mathrm{5}}{\mathrm{12}}+\frac{\mathrm{104}}{\mathrm{3}}−\mathrm{32}\:=\:\frac{\mathrm{5}}{\mathrm{12}}\:+\:\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$=\:\frac{\mathrm{37}}{\mathrm{12}}\bigstar\: \\ $$
Commented by bemath last updated on 30/Jun/20

$$\mathrm{thank} \\ $$
