
Question Number 101026 by 175 last updated on 29/Jun/20

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}}{{e}^{\:\mathrm{sin}{x}\:−{x}} } \\ $$
Answered by mathmax by abdo last updated on 29/Jun/20
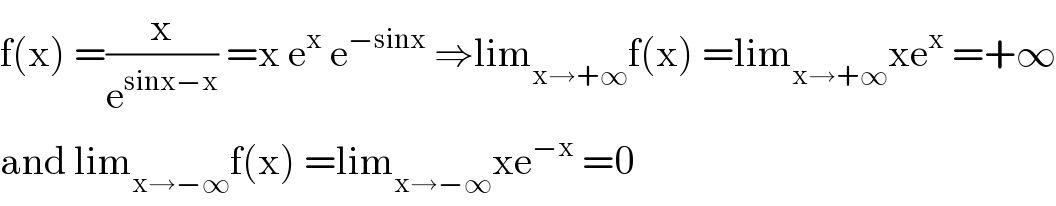
$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{sinx}−\mathrm{x}} }\:=\mathrm{x}\:\mathrm{e}^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{sinx}} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xe}^{\mathrm{x}} \:=+\infty \\ $$$$\mathrm{and}\:\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{xe}^{−\mathrm{x}} \:=\mathrm{0} \\ $$
