
Question Number 100956 by bobhans last updated on 29/Jun/20
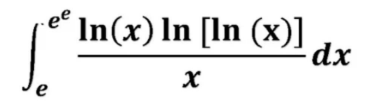
Answered by john santu last updated on 29/Jun/20
![set ln(x) = z → { ((z=1)),((z=e)) :} I= ∫_1 ^e ln(z). z dz = (1/2)z^2 .ln(z)]_1 ^e −(1/2)∫_1 ^e z dz = (e^2 /2) −[(1/4)z^2 ]_1 ^e = (e^2 /2)−[(e^2 /4)−(1/4)] =((e^2 +1)/(4 )) .](Q100959.png)
$$\mathrm{set}\:\mathrm{ln}\left(\mathrm{x}\right)\:=\:\mathrm{z}\:\rightarrow\begin{cases}{\mathrm{z}=\mathrm{1}}\\{\mathrm{z}=\mathrm{e}}\end{cases} \\ $$$$\left.\mathrm{I}=\:\underset{\mathrm{1}} {\overset{\mathrm{e}} {\int}}\:\mathrm{ln}\left(\mathrm{z}\right).\:\mathrm{z}\:\mathrm{dz}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{z}^{\mathrm{2}} .\mathrm{ln}\left(\mathrm{z}\right)\right]_{\mathrm{1}} ^{\mathrm{e}} −\frac{\mathrm{1}}{\mathrm{2}}\overset{\mathrm{e}} {\int}_{\mathrm{1}} \mathrm{z}\:\mathrm{dz}\:\: \\ $$$$=\:\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{2}}\:−\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{z}^{\mathrm{2}} \:\right]_{\mathrm{1}} ^{\mathrm{e}} =\:\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{2}}−\left[\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right] \\ $$$$=\frac{\mathrm{e}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}\:}\:. \\ $$
Commented by bobhans last updated on 29/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 29/Jun/20
![I =∫_e ^e^e ((ln(x)ln(lnx))/x)dx changement lnx =t give x =e^t ⇒ I =∫_1 ^e ((tln(t))/e^t )e^t dt =∫_1 ^e tln(t)dt =_(by parts) [(t^2 /2)ln(t)]_1 ^e +∫_1 ^e (t^2 /2)(dt/t) =(e^2 /2) +(1/2)[(t^2 /2)]_1 ^e =(e^2 /2) +(1/4)(e^2 −1) =(3/4)e^2 −(1/4)](Q100970.png)
$$\mathrm{I}\:=\int_{\mathrm{e}} ^{\mathrm{e}^{\mathrm{e}} } \frac{\mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{lnx}\right)}{\mathrm{x}}\mathrm{dx}\:\mathrm{changement}\:\mathrm{lnx}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}\:=\mathrm{e}^{\mathrm{t}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{tln}\left(\mathrm{t}\right)}{\mathrm{e}^{\mathrm{t}} }\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\mathrm{tln}\left(\mathrm{t}\right)\mathrm{dt}\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}\right)\right]_{\mathrm{1}} ^{\mathrm{e}} \:+\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\frac{\mathrm{dt}}{\mathrm{t}} \\ $$$$=\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{1}} ^{\mathrm{e}} \:=\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}^{\mathrm{2}} −\mathrm{1}\right)\:=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{e}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by john santu last updated on 29/Jun/20
![why [ (t^2 /2) ln(t) ]_1 ^e + ∫_1 ^e (t^2 /2) (dt/(t )) ?](Q100972.png)
$$\mathrm{why}\:\left[\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{ln}\left(\mathrm{t}\right)\:\right]_{\mathrm{1}} ^{\mathrm{e}} +\:\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\frac{\mathrm{dt}}{\mathrm{t}\:}\:?\: \\ $$$$ \\ $$
Commented by john santu last updated on 29/Jun/20
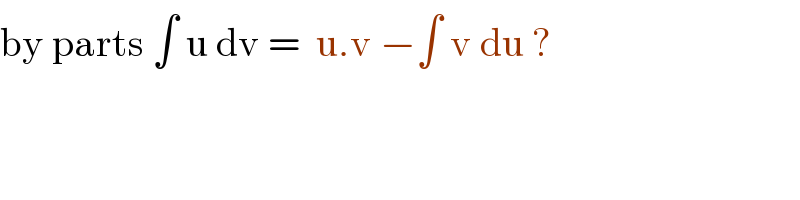
$$\mathrm{by}\:\mathrm{parts}\:\int\:\mathrm{u}\:\mathrm{dv}\:=\:\:\mathrm{u}.\mathrm{v}\:−\int\:\mathrm{v}\:\mathrm{du}\:? \\ $$
Commented by mathmax by abdo last updated on 29/Jun/20

$$\mathrm{integration}\:\mathrm{by}\:\mathrm{parts} \\ $$
Commented by mathmax by abdo last updated on 29/Jun/20
![sorry error of sign I =[(t^2 /2)lnt]_1 ^e −∫_1 ^e (t^2 /(2t))dt =....=(e^2 /2)−(1/4)(e^2 −1) =(1/4)e^2 +(1/4) =((e^2 +1)/4)](Q100989.png)
$$\mathrm{sorry}\:\mathrm{error}\:\mathrm{of}\:\mathrm{sign}\:\:\mathrm{I}\:=\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\mathrm{lnt}\right]_{\mathrm{1}} ^{\mathrm{e}} −\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2t}}\mathrm{dt} \\ $$$$=....=\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}^{\mathrm{2}} −\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}\:=\frac{\mathrm{e}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{4}} \\ $$
Commented by bobhans last updated on 29/Jun/20

$$\mathrm{yes}\:\mathrm{sir} \\ $$
