
Question Number 100928 by ajfour last updated on 29/Jun/20
Commented by ajfour last updated on 29/Jun/20
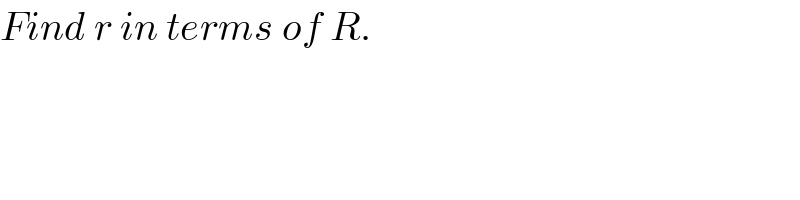
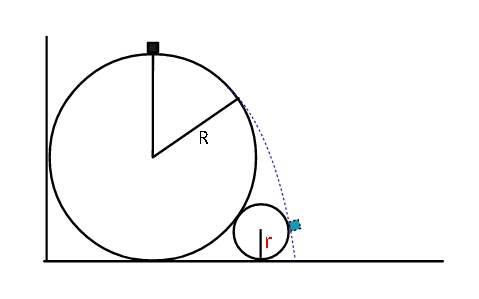
$${Find}\:{r}\:{in}\:{terms}\:{of}\:{R}. \\ $$
Commented by ajfour last updated on 30/Jun/20
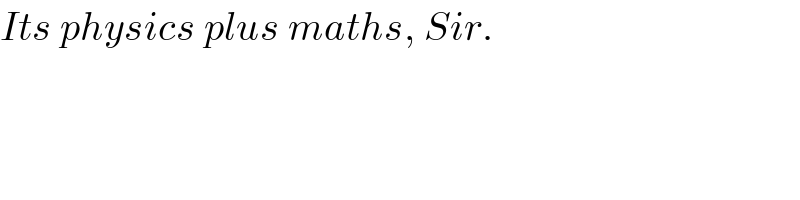
$${Its}\:{physics}\:{plus}\:{maths},\:{Sir}. \\ $$
Answered by bramlex last updated on 29/Jun/20
Commented by bramlex last updated on 29/Jun/20
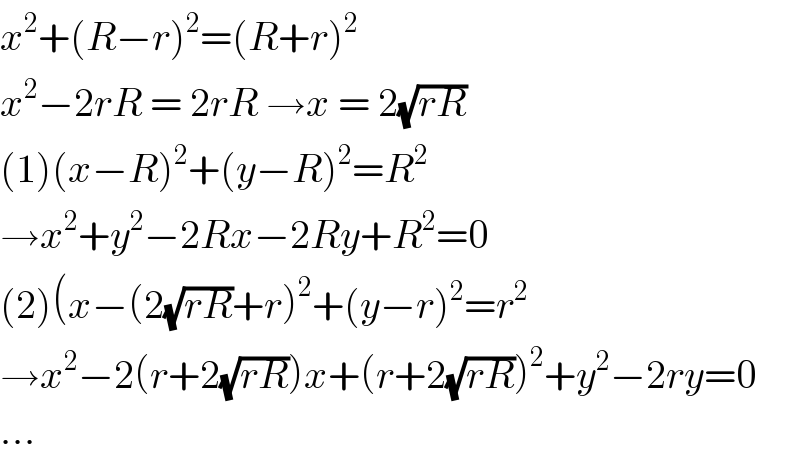
$${x}^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} =\left({R}+{r}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{rR}\:=\:\mathrm{2}{rR}\:\rightarrow{x}\:=\:\mathrm{2}\sqrt{{rR}} \\ $$$$\left(\mathrm{1}\right)\left({x}−{R}\right)^{\mathrm{2}} +\left({y}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{Rx}−\mathrm{2}{Ry}+{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\left({x}−\left(\mathrm{2}\sqrt{{rR}}+{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \right. \\ $$$$\rightarrow{x}^{\mathrm{2}} −\mathrm{2}\left({r}+\mathrm{2}\sqrt{{rR}}\right){x}+\left({r}+\mathrm{2}\sqrt{{rR}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{ry}=\mathrm{0} \\ $$$$... \\ $$
Answered by mr W last updated on 29/Jun/20
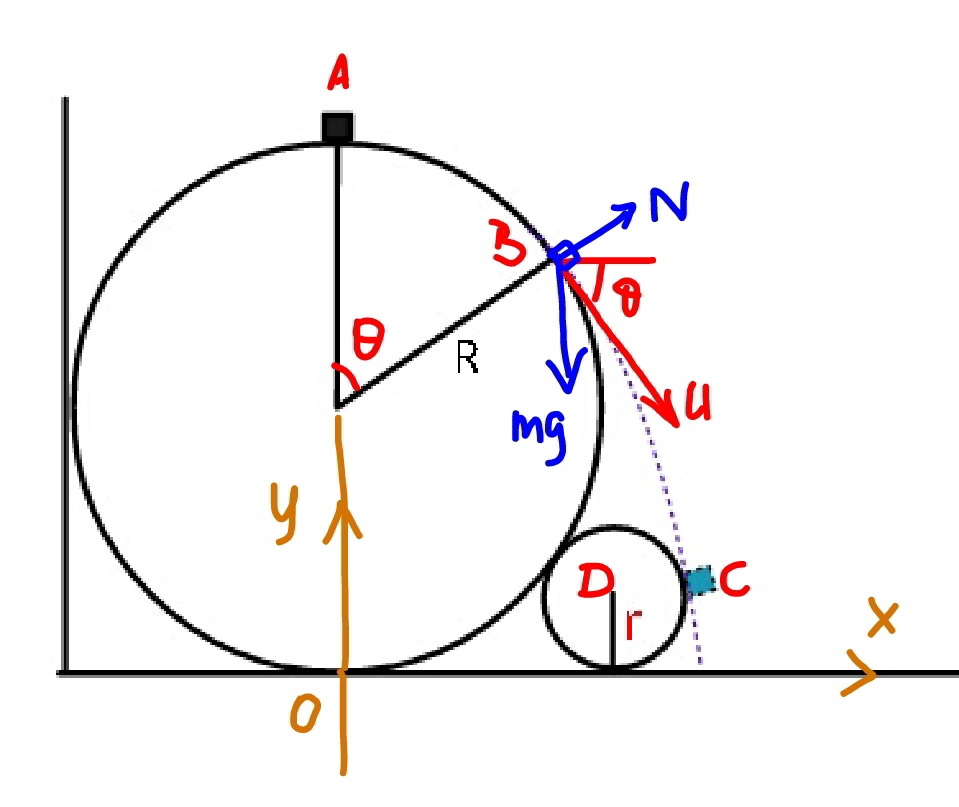
Commented by mr W last updated on 29/Jun/20

$${at}\:{position}\:\theta: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mu}^{\mathrm{2}} ={R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right){mg} \\ $$$$\Rightarrow{u}=\sqrt{\mathrm{2}{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right){g}} \\ $$$${mg}\:\mathrm{cos}\:\theta−{N}=\frac{{mu}^{\mathrm{2}} }{{R}} \\ $$$${N}=\mathrm{0}\:{when}\:{contact}\:{gets}\:{lost} \\ $$$${mg}\:\mathrm{cos}\:\theta=\frac{{m}×\mathrm{2}{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right){g}}{{R}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{u}=\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}} \\ $$$${track}\:{of}\:{mass}\:{m}\:{after}\:{point}\:{B}: \\ $$$${x}={R}\:\mathrm{sin}\:\theta+{u}\:\mathrm{cos}\:\theta\:{t} \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}{t} \\ $$$${y}={R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)−{u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{5}{R}}{\mathrm{3}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${D}\left(\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} },\:{r}\right)\equiv{D}\left(\mathrm{2}\sqrt{{Rr}},{r}\right) \\ $$$${let}\:\Phi={DC}^{\mathrm{2}} \\ $$$$\Phi=\left({x}−\mathrm{2}\sqrt{{Rr}}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} \\ $$$$\Phi=\left(\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}{t}−\mathrm{2}\sqrt{{Rr}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{5}{R}}{\mathrm{3}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} \\ $$$$\frac{{d}\Phi}{{dt}}=\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}{t}−\mathrm{2}\sqrt{{Rr}}\right)\left(\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}\right)+\mathrm{2}\left(\frac{\mathrm{5}{R}}{\mathrm{3}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} −{r}\right)\left(−\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{Rg}}{\mathrm{3}}}−{gt}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{12}\left(\sqrt{\mathrm{30}}+\mathrm{4}\sqrt{\frac{{g}}{{R}}}{t}−\mathrm{6}\sqrt{\mathrm{6}}\sqrt{\frac{{r}}{{R}}}\right)=\left(\mathrm{30}−\mathrm{2}\sqrt{\mathrm{30}}\sqrt{\frac{{g}}{{R}}}\:{t}−\mathrm{9}\left(\sqrt{\frac{{g}}{{R}}}{t}\right)^{\mathrm{2}} −\mathrm{18}\frac{{r}}{{R}}\right)\left(\sqrt{\mathrm{30}}+\mathrm{9}\sqrt{\frac{{g}}{{R}}}{t}\right) \\ $$$$\Phi_{{min}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{9}}\sqrt{\frac{{g}}{{R}}}{t}−\mathrm{2}\sqrt{\frac{{r}}{{R}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{3}}−\frac{\sqrt{\mathrm{30}}}{\mathrm{9}}\sqrt{\frac{{g}}{{R}}}\:{t}−\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\frac{{g}}{{R}}}{t}\right)^{\mathrm{2}} −\frac{{r}}{{R}}\right)^{\mathrm{2}} =\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} \\ $$$${let}\:\delta=\sqrt{\frac{{g}}{{R}}}{t},\:\lambda=\sqrt{\frac{{r}}{{R}}} \\ $$$$\Rightarrow\mathrm{12}\left(\sqrt{\mathrm{30}}+\mathrm{4}\delta−\mathrm{6}\sqrt{\mathrm{6}}\lambda\right)=\left(\mathrm{30}−\mathrm{2}\sqrt{\mathrm{30}}\delta−\mathrm{9}\delta^{\mathrm{2}} −\mathrm{18}\lambda^{\mathrm{2}} \right)\left(\sqrt{\mathrm{30}}+\mathrm{9}\delta\right)\:\:\:...\left({i}\right) \\ $$$$\Rightarrow\mathrm{4}\left(\mathrm{3}\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{6}}\delta−\mathrm{18}\lambda\right)^{\mathrm{2}} +\left(\mathrm{30}−\mathrm{2}\sqrt{\mathrm{30}}\delta−\mathrm{9}\delta^{\mathrm{2}} −\mathrm{18}\lambda^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{324}\lambda^{\mathrm{4}} \:\:\:...\left({ii}\right) \\ $$$${we}\:{get}\:{from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\lambda\approx\mathrm{0}.\mathrm{53716} \\ $$$$\Rightarrow{r}=\lambda^{\mathrm{2}} {R}\approx\mathrm{0}.\mathrm{2885}{R} \\ $$
Commented by mr W last updated on 29/Jun/20
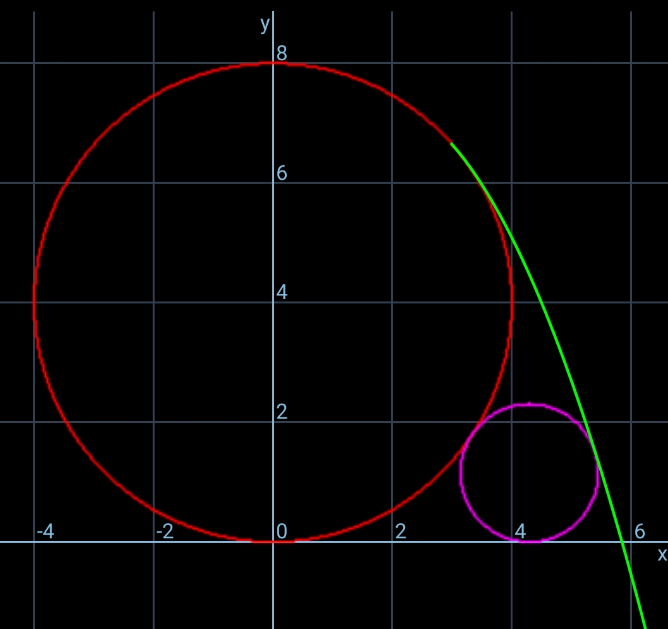
Commented by ajfour last updated on 29/Jun/20

$${haven}'{t}\:{been}\:{through}\:{all}\:{of}\:{it}\:{sir},\:{but} \\ $$$${really}\:{looks}\:{superb}\:{solution},\:{i}\:{want} \\ $$$${to}\:{try}\:{on}\:{my}\:{own}\:{for}\:{a}\:{little}\:{while}... \\ $$
Commented by ajfour last updated on 29/Jun/20

$${can}\:{you}\:{help}\:{me}\:{sir},\:{with}\:{the}\:{equation} \\ $$$${of}\:{parabola}\:{with}\:{shown}\:{axes}..? \\ $$
Commented by mr W last updated on 30/Jun/20
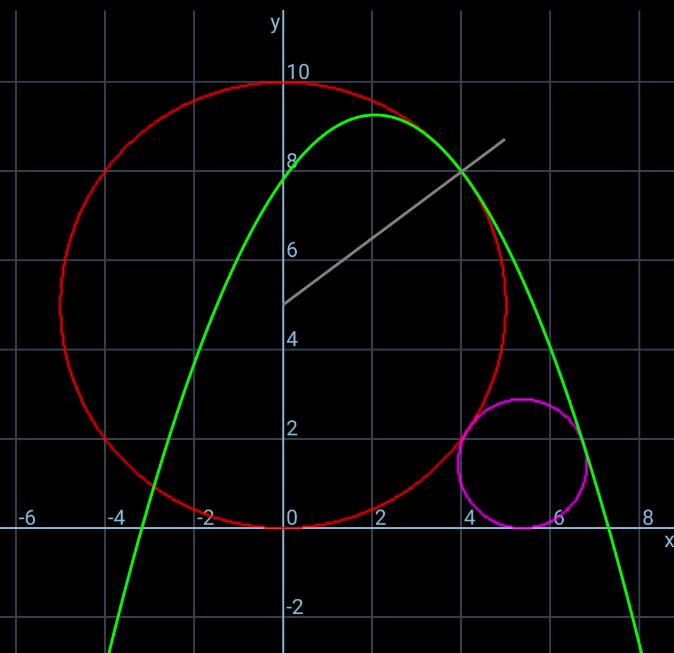
Commented by ajfour last updated on 02/Jul/20
![x=Rsin θ+(ucos θ)t y=R(1+cos θ)−(usin θ)t−((gt^2 )/2) As cos θ=(2/3) , sin θ=((√5)/3) , u^2 =((2Rg)/3) y=((5R)/3)−(((u(√5))/3))(((x−((R(√5))/3)))/((((2u)/3))))−(g/2)(((x−((R(√5))/3))^2 )/((((2u)/3))^2 )) y=((5R)/3)−((√5)/2)(x−((R(√5))/3))−((27)/(16R))(x−((R(√5))/3))^2 (dy/dx)=−((√5)/2)−((27)/(8R))(x−((R(√5))/3))=0 ⇒ x_0 =((R(√5))/3)−((8R)/(27))(((√5)/2)) = ((5(√5)R)/(27)) y_0 =((5R)/3)−((√5)/2)(((5(√5)R)/(27))−((9R(√5))/(27))) −((27)/(16R))(((80R^2 )/(27×27))) ⇒ y_0 =((5R)/3)+((10R)/(27))−((5R)/(27))=((50R)/(27)) < 2R Thus eq. of parabola is y=((50R)/(27))−((27)/(16R))(x−((5(√5)R)/(27)))^2 (dy/dx)=−((27)/(8R))(x−((5(√5)R)/(27))) say this parabola touches the smaller circle at P (h,k) and let center of smaller circle is C(2(√(Rr)), r); then h=2(√(Rr))+rcos 𝛃 k=r+rsin 𝛃 cot β=((27)/(8R))(h−((5(√5)R)/(27)))=((h−2(√(Rr)))/(k−r)) ⇒ ((27)/8)z=(((z+((5(√5))/(27)))−2(√s))/(((50)/(27))−((27)/(16))z^2 −s)) ......(i) k=((50R)/(27))−((27)/(16R))(h−((5(√5)R)/(27)))^2 = r+(r/((1+[((27)/(8R))(h−((5(√5)R)/(27)))]^2 ))^(1/) ) ⇒ ((50)/(27))−((27)/(16))z^2 =s+(s/((1+(((27)/(16))z)^2 ))^(1/) ) .....(ii) ⇒ s=(((((50)/(27))−((27)/(16))z^2 ))/(1+(1/((1+(((27z)/(16)))^2 ))^(1/) ))) ; Now ⇒ ((27)/8)z=(((z+((5(√5))/(27)))−2{(((((50)/(27))−((27)/(16))z^2 ))/(1+(1/((1+(((27z)/(16)))^2 ))^(1/) )))}^(1/2) )/(((50)/(27))−((27)/(16))z^2 −((((((50)/(27))−((27)/(16))z^2 ))/(1+(1/((1+(((27z)/(16)))^2 ))^(1/) )))))) ......(A) z is obtained from above eq. Then s=(r/R) = (((((50)/(27))−((27)/(16))z^2 ))/(1+(1/((1+(((27z)/(16)))^2 ))^(1/) ))) ■](Q101092.png)
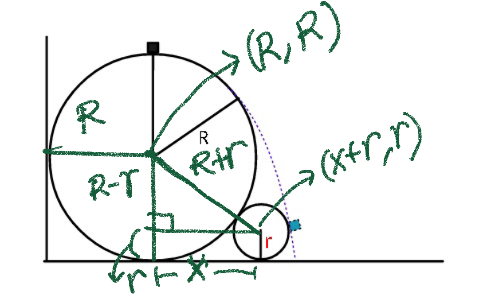
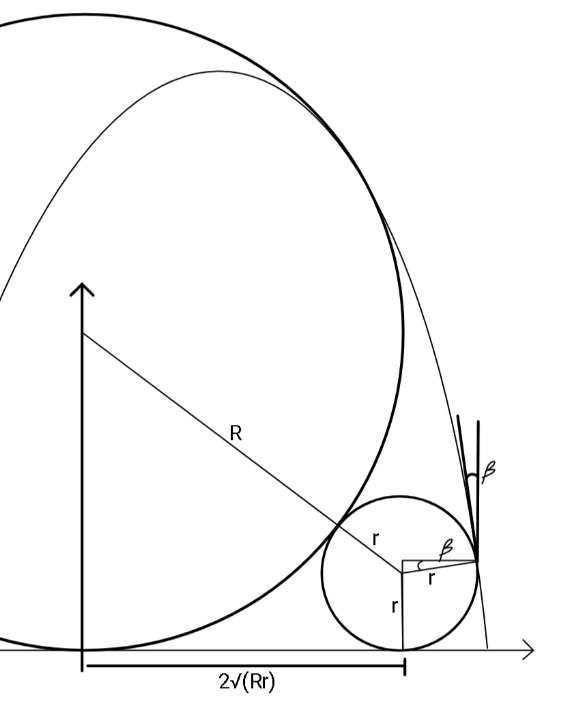
$${x}={R}\mathrm{sin}\:\theta+\left({u}\mathrm{cos}\:\theta\right){t} \\ $$$${y}={R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)−\left({u}\mathrm{sin}\:\theta\right){t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${As}\:\:\mathrm{cos}\:\theta=\frac{\mathrm{2}}{\mathrm{3}}\:,\:\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\:,\:{u}^{\mathrm{2}} =\frac{\mathrm{2}{Rg}}{\mathrm{3}} \\ $$$${y}=\frac{\mathrm{5}{R}}{\mathrm{3}}−\left(\frac{{u}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)\frac{\left({x}−\frac{{R}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)}{\left(\frac{\mathrm{2}{u}}{\mathrm{3}}\right)}−\frac{{g}}{\mathrm{2}}\frac{\left({x}−\frac{{R}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)^{\mathrm{2}} }{\left(\frac{\mathrm{2}{u}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$${y}=\frac{\mathrm{5}{R}}{\mathrm{3}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left({x}−\frac{{R}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)−\frac{\mathrm{27}}{\mathrm{16}{R}}\left({x}−\frac{{R}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\mathrm{27}}{\mathrm{8}{R}}\left({x}−\frac{{R}\sqrt{\mathrm{5}}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}_{\mathrm{0}} =\frac{{R}\sqrt{\mathrm{5}}}{\mathrm{3}}−\frac{\mathrm{8}{R}}{\mathrm{27}}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{5}\sqrt{\mathrm{5}}{R}}{\mathrm{27}} \\ $$$${y}_{\mathrm{0}} =\frac{\mathrm{5}{R}}{\mathrm{3}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left(\frac{\mathrm{5}\sqrt{\mathrm{5}}{R}}{\mathrm{27}}−\frac{\mathrm{9}{R}\sqrt{\mathrm{5}}}{\mathrm{27}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{27}}{\mathrm{16}{R}}\left(\frac{\mathrm{80}{R}^{\mathrm{2}} }{\mathrm{27}×\mathrm{27}}\right) \\ $$$$\Rightarrow\:{y}_{\mathrm{0}} =\frac{\mathrm{5}{R}}{\mathrm{3}}+\frac{\mathrm{10}{R}}{\mathrm{27}}−\frac{\mathrm{5}{R}}{\mathrm{27}}=\frac{\mathrm{50}{R}}{\mathrm{27}}\:\:<\:\mathrm{2}{R} \\ $$$${Thus}\:{eq}.\:{of}\:{parabola}\:{is} \\ $$$$\:\:\boldsymbol{{y}}=\frac{\mathrm{50}\boldsymbol{{R}}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}\boldsymbol{{R}}}\left(\boldsymbol{{x}}−\frac{\mathrm{5}\sqrt{\mathrm{5}}\boldsymbol{{R}}}{\mathrm{27}}\right)^{\mathrm{2}} \\ $$$$\:\:\frac{{dy}}{{dx}}=−\frac{\mathrm{27}}{\mathrm{8}{R}}\left({x}−\frac{\mathrm{5}\sqrt{\mathrm{5}}{R}}{\mathrm{27}}\right) \\ $$$${say}\:{this}\:{parabola}\:{touches}\:{the}\:{smaller} \\ $$$${circle}\:{at}\:{P}\:\left({h},{k}\right)\:\:{and}\:{let}\:{center}\:{of} \\ $$$${smaller}\:{circle}\:{is}\:{C}\left(\mathrm{2}\sqrt{{Rr}},\:{r}\right);\:\:{then} \\ $$$${h}=\mathrm{2}\sqrt{{Rr}}+{r}\mathrm{cos}\:\boldsymbol{\beta} \\ $$$${k}={r}+{r}\mathrm{sin}\:\boldsymbol{\beta} \\ $$$$\mathrm{cot}\:\beta=\frac{\mathrm{27}}{\mathrm{8}{R}}\left({h}−\frac{\mathrm{5}\sqrt{\mathrm{5}}{R}}{\mathrm{27}}\right)=\frac{{h}−\mathrm{2}\sqrt{{Rr}}}{{k}−{r}} \\ $$$$ \\ $$$$\Rightarrow\:\:\:\:\:\frac{\mathrm{27}}{\mathrm{8}}{z}=\frac{\left({z}+\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{27}}\right)−\mathrm{2}\sqrt{{s}}}{\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} −{s}}\:\:\:\:\:\:\:......\left({i}\right) \\ $$$$ \\ $$$$\:\:{k}=\frac{\mathrm{50}{R}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}{R}}\left({h}−\frac{\mathrm{5}\sqrt{\mathrm{5}}{R}}{\mathrm{27}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:{r}+\frac{{r}}{\sqrt[{}]{\mathrm{1}+\left[\frac{\mathrm{27}}{\mathrm{8}{R}}\left({h}−\frac{\mathrm{5}\sqrt{\mathrm{5}}{R}}{\mathrm{27}}\right)\right]^{\mathrm{2}} }} \\ $$$$ \\ $$$$\Rightarrow\:\:\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} ={s}+\frac{{s}}{\sqrt[{}]{\mathrm{1}+\left(\frac{\mathrm{27}}{\mathrm{16}}{z}\right)^{\mathrm{2}} }}\:\:.....\left({ii}\right) \\ $$$$\Rightarrow\:\:{s}=\frac{\left(\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} \right)}{\mathrm{1}+\frac{\mathrm{1}}{\sqrt[{}]{\mathrm{1}+\left(\frac{\mathrm{27}{z}}{\mathrm{16}}\right)^{\mathrm{2}} }}}\:\:\:\:\:\:;\:\:\:{Now} \\ $$$$\Rightarrow\:\:\:\:\:\frac{\mathrm{27}}{\mathrm{8}}{z}=\frac{\left({z}+\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{27}}\right)−\mathrm{2}\left\{\frac{\left(\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} \right)}{\mathrm{1}+\frac{\mathrm{1}}{\sqrt[{}]{\mathrm{1}+\left(\frac{\mathrm{27}{z}}{\mathrm{16}}\right)^{\mathrm{2}} }}}\right\}^{\mathrm{1}/\mathrm{2}} }{\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} −\left(\frac{\left(\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} \right)}{\mathrm{1}+\frac{\mathrm{1}}{\sqrt[{}]{\mathrm{1}+\left(\frac{\mathrm{27}{z}}{\mathrm{16}}\right)^{\mathrm{2}} }}}\right)}\:\:\:\:\:\:\:......\left({A}\right) \\ $$$${z}\:{is}\:{obtained}\:{from}\:{above}\:{eq}. \\ $$$${Then}\:\:\:{s}=\frac{{r}}{{R}}\:=\:\frac{\left(\frac{\mathrm{50}}{\mathrm{27}}−\frac{\mathrm{27}}{\mathrm{16}}{z}^{\mathrm{2}} \right)}{\mathrm{1}+\frac{\mathrm{1}}{\sqrt[{}]{\mathrm{1}+\left(\frac{\mathrm{27}{z}}{\mathrm{16}}\right)^{\mathrm{2}} }}}\:\:\blacksquare \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 02/Jul/20
Commented by mr W last updated on 02/Jul/20

$${beautifully}\:{solved}! \\ $$
