
Question Number 100792 by bramlex last updated on 28/Jun/20
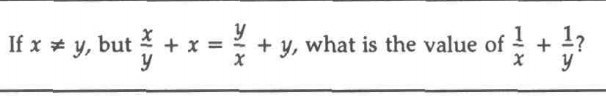
Answered by bobhans last updated on 28/Jun/20
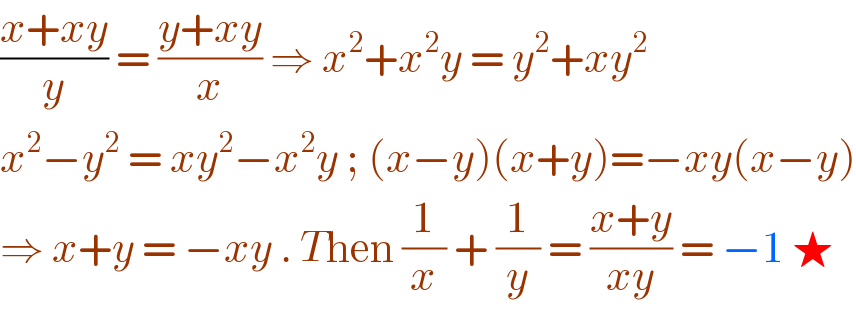
$$\frac{{x}+{xy}}{{y}}\:=\:\frac{{y}+{xy}}{{x}}\:\Rightarrow\:{x}^{\mathrm{2}} +{x}^{\mathrm{2}} {y}\:=\:{y}^{\mathrm{2}} +{xy}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:{xy}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}\:;\:\left({x}−{y}\right)\left({x}+{y}\right)=−{xy}\left({x}−{y}\right) \\ $$$$\Rightarrow\:{x}+{y}\:=\:−{xy}\:.\:{T}\mathrm{hen}\:\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{y}}\:=\:\frac{{x}+{y}}{{xy}}\:=\:−\mathrm{1}\:\bigstar \\ $$
