
Question Number 100491 by bobhans last updated on 27/Jun/20
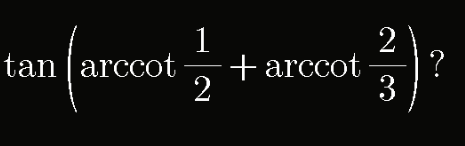
Answered by bramlex last updated on 27/Jun/20
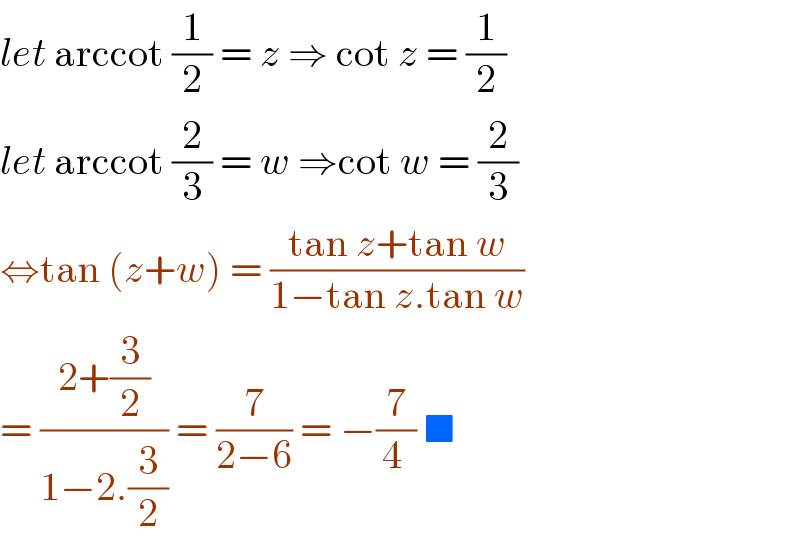
$${let}\:\mathrm{arccot}\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:{z}\:\Rightarrow\:\mathrm{cot}\:{z}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${let}\:\mathrm{arccot}\:\frac{\mathrm{2}}{\mathrm{3}}\:=\:{w}\:\Rightarrow\mathrm{cot}\:{w}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{tan}\:\left({z}+{w}\right)\:=\:\frac{\mathrm{tan}\:{z}+\mathrm{tan}\:{w}}{\mathrm{1}−\mathrm{tan}\:{z}.\mathrm{tan}\:{w}} \\ $$$$=\:\frac{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}}}{\mathrm{1}−\mathrm{2}.\frac{\mathrm{3}}{\mathrm{2}}}\:=\:\frac{\mathrm{7}}{\mathrm{2}−\mathrm{6}}\:=\:−\frac{\mathrm{7}}{\mathrm{4}\:}\:\blacksquare\: \\ $$
