
Question Number 100378 by bemath last updated on 26/Jun/20
Commented by bemath last updated on 26/Jun/20
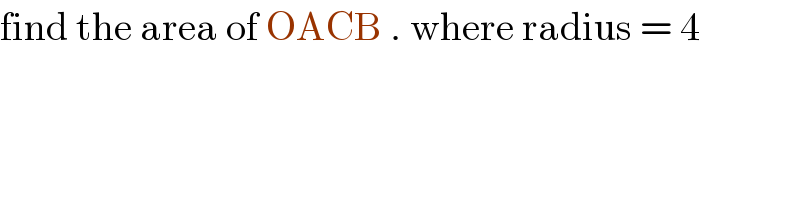
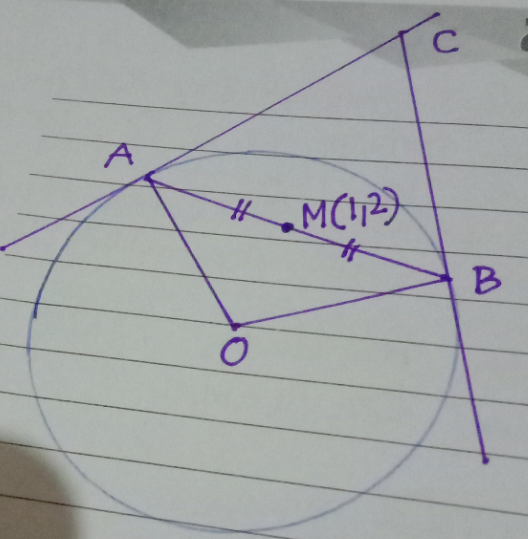
$$\mathrm{find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{OACB}\:.\:\mathrm{where}\:\mathrm{radius}\:=\:\mathrm{4} \\ $$
Answered by john santu last updated on 26/Jun/20
Commented by john santu last updated on 26/Jun/20
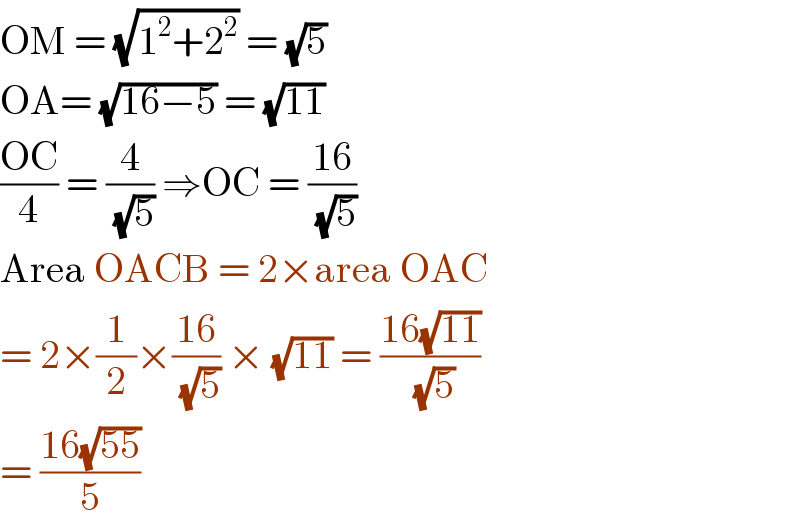
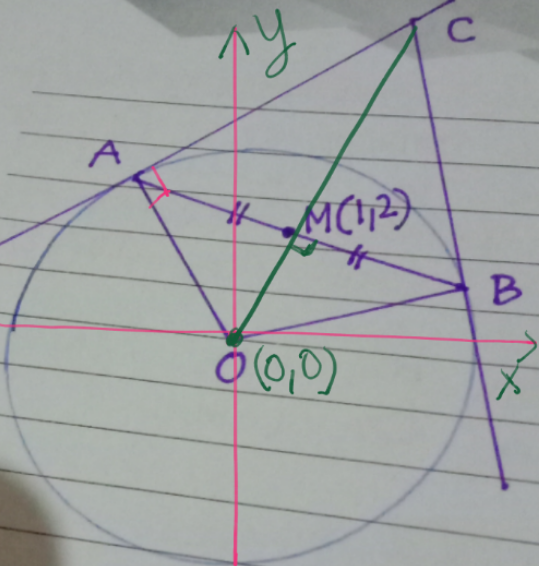
$$\mathrm{OM}\:=\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{5}} \\ $$$$\mathrm{OA}=\:\sqrt{\mathrm{16}−\mathrm{5}}\:=\:\sqrt{\mathrm{11}} \\ $$$$\frac{\mathrm{OC}}{\mathrm{4}}\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{OC}\:=\:\frac{\mathrm{16}}{\sqrt{\mathrm{5}}} \\ $$$$\mathrm{Area}\:\mathrm{OACB}\:=\:\mathrm{2}×\mathrm{area}\:\mathrm{OAC} \\ $$$$=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{16}}{\sqrt{\mathrm{5}}}\:×\:\sqrt{\mathrm{11}}\:=\:\frac{\mathrm{16}\sqrt{\mathrm{11}}}{\sqrt{\mathrm{5}}} \\ $$$$=\:\frac{\mathrm{16}\sqrt{\mathrm{55}}}{\mathrm{5}}\: \\ $$
Commented by bemath last updated on 26/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
