
Question Number 100216 by Rio Michael last updated on 25/Jun/20
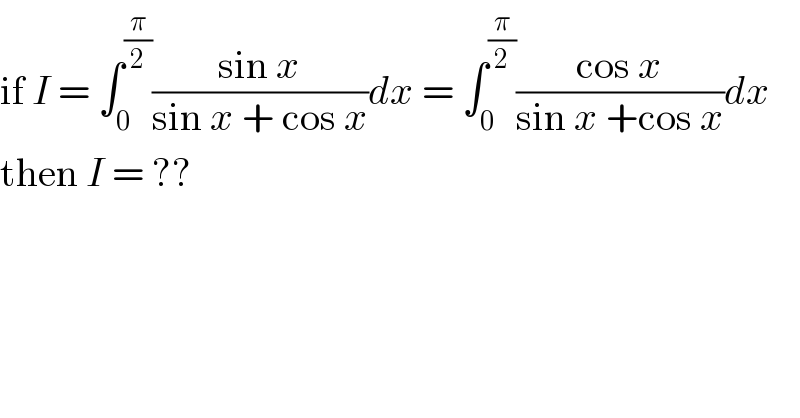
$$\mathrm{if}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}}{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx}\: \\ $$$$\mathrm{then}\:{I}\:=\:?? \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20
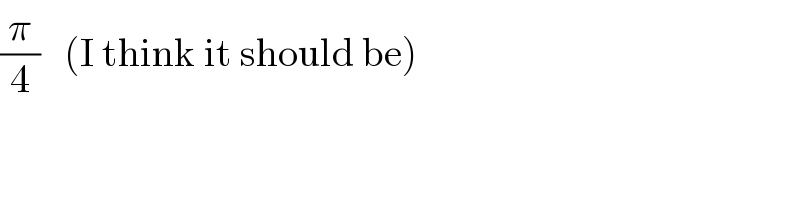
$$\frac{\pi}{\mathrm{4}}\:\:\:\left(\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20
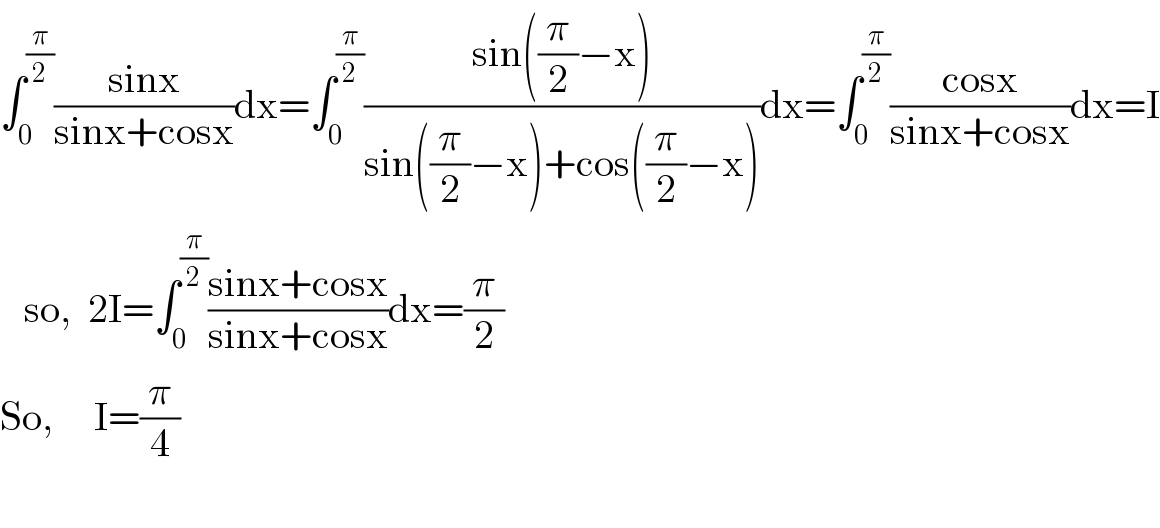
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}\mathrm{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\mathrm{I} \\ $$$$\:\:\:\mathrm{so},\:\:\mathrm{2I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}+\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{So},\:\:\:\:\:\mathrm{I}=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 25/Jun/20
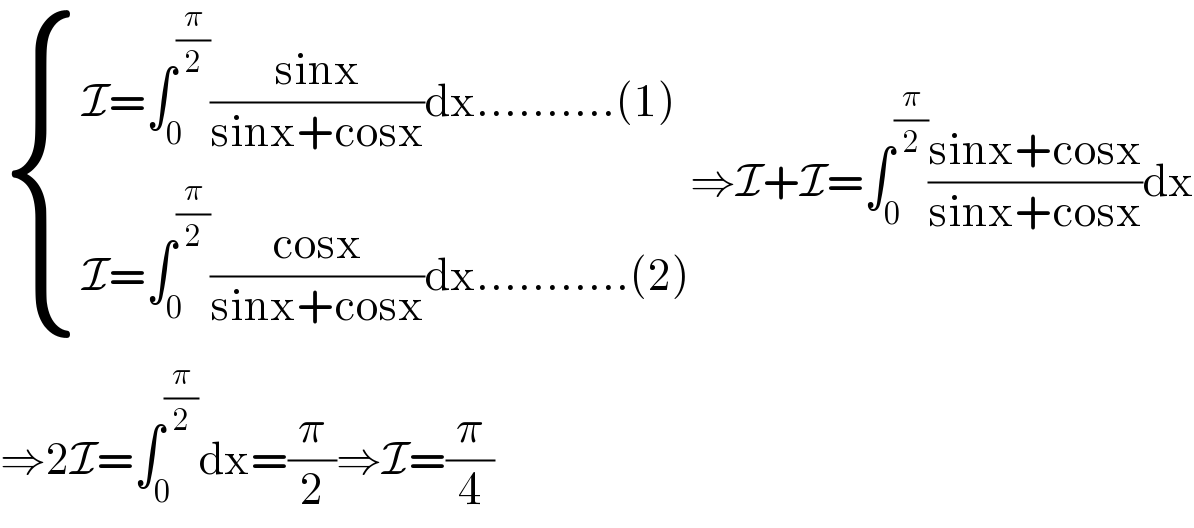
$$\begin{cases}{\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}..........\left(\mathrm{1}\right)}\\{\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}...........\left(\mathrm{2}\right)}\end{cases}\Rightarrow\mathcal{I}+\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}+\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx} \\ $$$$\Rightarrow\mathrm{2}\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{dx}=\frac{\pi}{\mathrm{2}}\Rightarrow\mathcal{I}=\frac{\pi}{\mathrm{4}} \\ $$
Commented by Coronavirus last updated on 25/Jun/20

$${clean} \\ $$
Commented by Ar Brandon last updated on 25/Jun/20
Ouais
Commented by Rio Michael last updated on 26/Jun/20

$$\mathrm{thank}\:\mathrm{you}'\mathrm{ll} \\ $$
