
Question Number 100158 by Algoritm last updated on 25/Jun/20
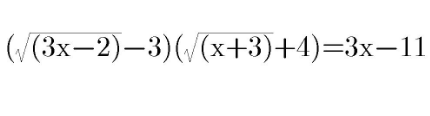
Answered by MJS last updated on 25/Jun/20

$${u}=\sqrt{{x}+\mathrm{3}}\:\Leftrightarrow\:{x}={u}^{\mathrm{2}} −\mathrm{3}\wedge{u}\geqslant\mathrm{0} \\ $$$$\left.\left(\left.{u}+\mathrm{4}\right)\right)\sqrt{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{11}}−\mathrm{3}\right)=\mathrm{3}{u}^{\mathrm{2}} −\mathrm{20} \\ $$$$\left({u}+\mathrm{4}\right)\sqrt{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{11}}=\mathrm{3}{u}^{\mathrm{2}} +\mathrm{3}{u}−\mathrm{8} \\ $$$${u}^{\mathrm{4}} −{u}^{\mathrm{3}} −\frac{\mathrm{38}}{\mathrm{3}}{u}^{\mathrm{2}} +\frac{\mathrm{20}}{\mathrm{3}}{u}+\mathrm{40}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{40} \\ $$$$\Rightarrow\:{u}_{\mathrm{1}} =\mathrm{3}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{6} \\ $$$${u}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{2}} −\frac{\mathrm{20}}{\mathrm{3}}{u}−\frac{\mathrm{40}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{trying}\:\Rightarrow\:{u}_{\mathrm{2}} =−\mathrm{2}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{because}\:{u}\geqslant\mathrm{0} \\ $$$${u}^{\mathrm{2}} −\frac{\mathrm{20}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:{u}_{\mathrm{3},\:\mathrm{4}} =\pm\frac{\mathrm{2}\sqrt{\mathrm{15}}}{\mathrm{3}}\:\Rightarrow\:{x}_{\mathrm{2}} =\frac{\mathrm{11}}{\mathrm{3}} \\ $$
