
Question Number 100036 by bobhans last updated on 24/Jun/20
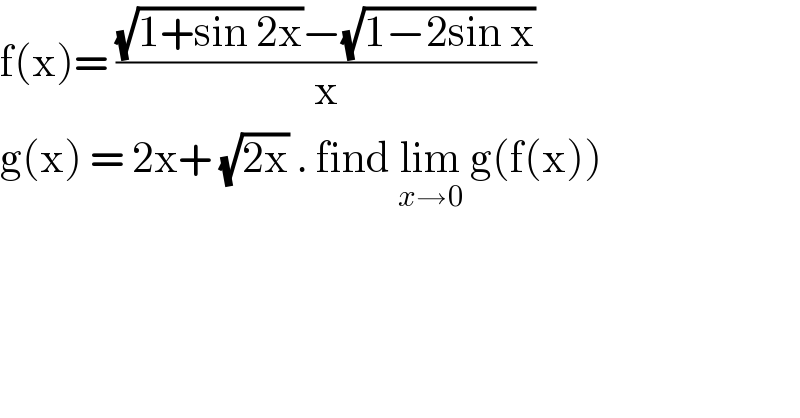
$$\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}−\sqrt{\mathrm{1}−\mathrm{2sin}\:\mathrm{x}}}{\mathrm{x}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\:\mathrm{2x}+\:\sqrt{\mathrm{2x}}\:.\:\mathrm{find}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$
Answered by john santu last updated on 24/Jun/20
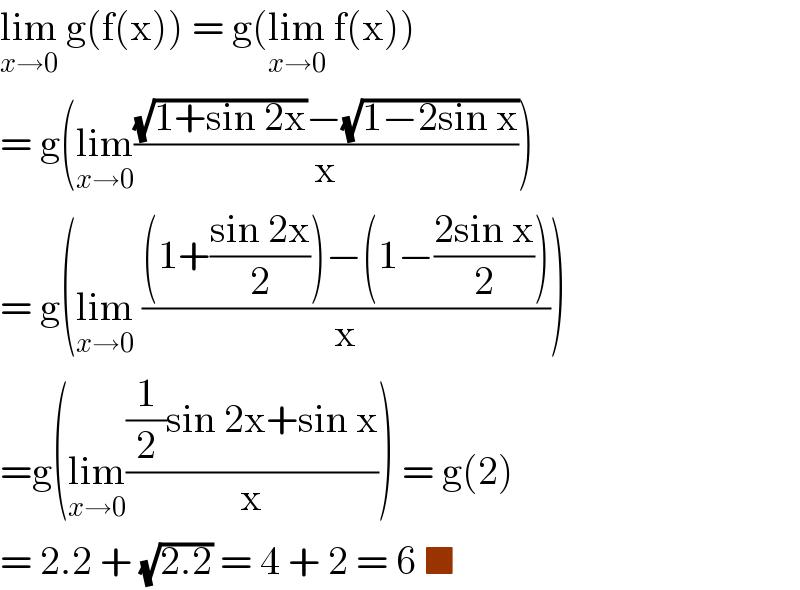
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\:\mathrm{g}\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$=\:\mathrm{g}\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}−\sqrt{\mathrm{1}−\mathrm{2sin}\:\mathrm{x}}}{\mathrm{x}}\right) \\ $$$$=\:\mathrm{g}\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{2}}\right)−\left(\mathrm{1}−\frac{\mathrm{2sin}\:\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{x}}\right) \\ $$$$=\mathrm{g}\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2x}+\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)\:=\:\mathrm{g}\left(\mathrm{2}\right) \\ $$$$=\:\mathrm{2}.\mathrm{2}\:+\:\sqrt{\mathrm{2}.\mathrm{2}}\:=\:\mathrm{4}\:+\:\mathrm{2}\:=\:\mathrm{6}\:\blacksquare \\ $$
