
Question Number 100027 by bemath last updated on 24/Jun/20
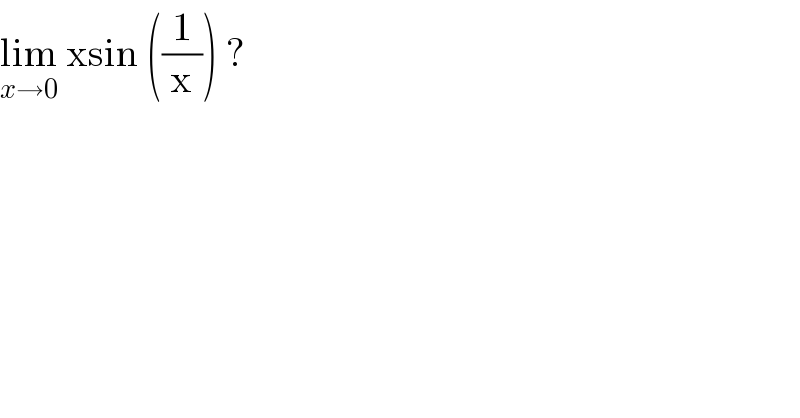
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{xsin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:?\: \\ $$
Commented by john santu last updated on 24/Jun/20
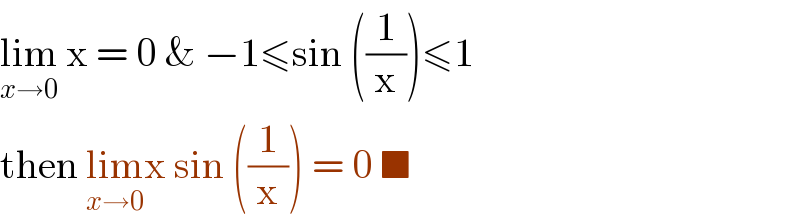
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{x}\:=\:\mathrm{0}\:\&\:−\mathrm{1}\leqslant\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}x}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\:\mathrm{0}\:\blacksquare \\ $$
Commented by bobhans last updated on 24/Jun/20
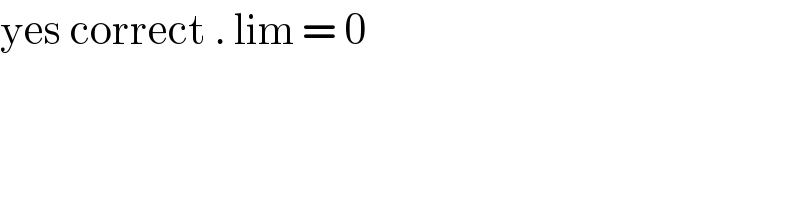
$$\mathrm{yes}\:\mathrm{correct}\:.\:\mathrm{lim}\:=\:\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 24/Jun/20
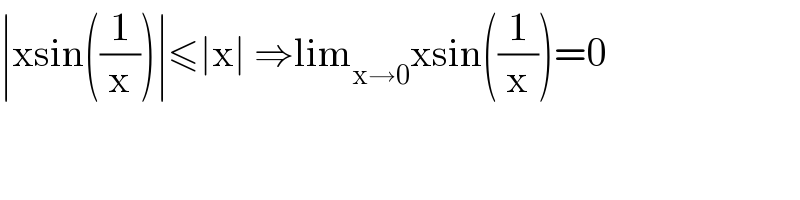
$$\mid\mathrm{xsin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\mid\leqslant\mid\mathrm{x}\mid\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{xsin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{0} \\ $$
