
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 218310 by mr W last updated on 06/Apr/25

$$\mathrm{10}\:{couples}\:{are}\:{invited}\:{to}\:{a}\:{dinner} \\ $$$${and}\:{should}\:{be}\:{seated}\:{at}\:{a}\:{round}\:{table}. \\ $$$${in}\:{how}\:{many}\:{ways}\:{can}\:{the}\:{host}\:{do} \\ $$$${this}, \\ $$$$\left.\mathrm{1}\right)\:{generally}. \\ $$$$\left.\mathrm{2}\right)\:{if}\:{the}\:{husband}\:{and}\:{the}\:{wife}\:{of} \\ $$$$\:\:\:\:\:{each}\:{couple}\:{should}\:{sit}\:{together}. \\ $$$$\left.\mathrm{3}\right)\:{if}\:{no}\:{two}\:{men}\:{should}\:{sit}\:{next} \\ $$$$\:\:\:\:\:{to}\:{each}\:{other}. \\ $$$$\left.\mathrm{4}\left.\right)\:{as}\:\mathrm{3}\right),\:{but}\:{two}\:{speicial}\:{couples}\: \\ $$$$\:\:\:\:\:{should}\:{not}\:{sit}\:{next}\:{to}\:{each}\:{other}. \\ $$$$\:\:\:\:\underline{\:{it}\:{means}\:}{that}\:{the}\:{husband}\:{from}\: \\ $$$$\:\:\:\:\:{couple}\:\mathrm{1}\:{may}\:{not}\:{sit}\:{next}\:{to}\:{the} \\ $$$$\:\:\:\:\:{wife}\:{from}\:{couple}\:\mathrm{2}\:{and}\:{the} \\ $$$$\:\:\:\:\:\:{husband}\:{from}\:{couple}\:\mathrm{2}\:{may}\:{not} \\ $$$$\:\:\:\:\:\:{sit}\:{next}\:{to}\:{the}\:{wife}\:{from}\:{couple}\:\mathrm{1}. \\ $$$$\:\:\:\:\:\:{but}\:{certainly}\:{the}\:{husbands}\:{of} \\ $$$$\:\:\:\:\:\:{both}\:{couples}\:{may}\:{sit}\:{next}\:{to}\:{their} \\ $$$$\:\:\:\:\:\:{own}\:{wifes}. \\ $$
Commented by nikif99 last updated on 08/Apr/25
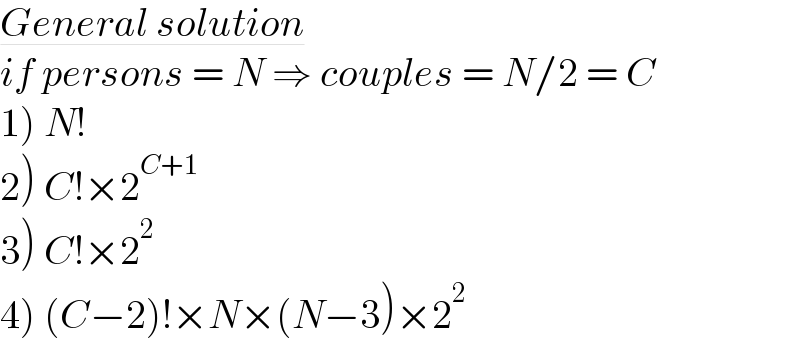
$$\underline{{General}\:{solution}} \\ $$$${if}\:{persons}\:=\:{N}\:\Rightarrow\:{couples}\:=\:{N}/\mathrm{2}\:=\:{C} \\ $$$$\left.\mathrm{1}\right)\:{N}! \\ $$$$\left.\mathrm{2}\right)\:{C}!×\mathrm{2}^{{C}+\mathrm{1}} \\ $$$$\left.\mathrm{3}\right)\:{C}!×\mathrm{2}^{\mathrm{2}} \\ $$$$\left.\mathrm{4}\right)\:\left({C}−\mathrm{2}\right)!×{N}×\left({N}−\mathrm{3}\right)×\mathrm{2}^{\mathrm{2}} \\ $$
Answered by nikif99 last updated on 08/Apr/25
![I try an answer (figure follows). 10 couples are 20 persons. 1) Arrangements of 20 people, even in circle, with different places are 20! 2) Couples must sit in adjacent places. Consider 10 twin seats (see Table A). There are 10! ways for 10 couples. Also, couple 1 can interchange seats (×2), couple 2 can do the same (×2),... till couple 10 (×2), e.g. 2^(10) . Also, all couples can shift one place (see red bracket) (×2). Total 10!∙2^(11) 3) (suppose restriction #2 plus...) ...No two men in adjacent places. If the pattern (mw−mw−mw−mw...) {where m man, w woman} changes to (mw−wm−wm−wm...) the circle doesn′t close normally. 10 couples are sitting in 10 twin seats in 10! ways (see Table B). Also, the pattern can change to (wm−wm−wm...) (×2). Also, all couples can shift one place (red bracket) (×2). Total 10!∙2^2 4) Restriction (3) plus not two certain couples next to each other. Consider two couples, red and blue, not allowed in adjacent seats (see Table C). Positions not allowed for those two couples are 10−1 (^a ). Remaining 8 couples are sitted in 8! ways (^b ). Also these two couples are not allowed at first and last positions, where table ends (see red bracket), so remaining 8 couples have another 8! ways of sitting (^c ). Also, couples can interchange seats ×2 (^d ). Knowing all arrangements are 10!, above exceptions are deducted. 10!−2_(d) ∙(10−1)_(a) (10−2)!_(b) −2_(d) ∙(10−2)!_(c) = 10!−(10−2)![2(10−1)+2]= 10!−2∙10(10−2)!=10∙(10−3)(10−2)! Finally, cases allowed must ×2 for interchanging seats, ×2 for shifting one place. Total 8!∙10∙7∙2^2](Q218390.png)
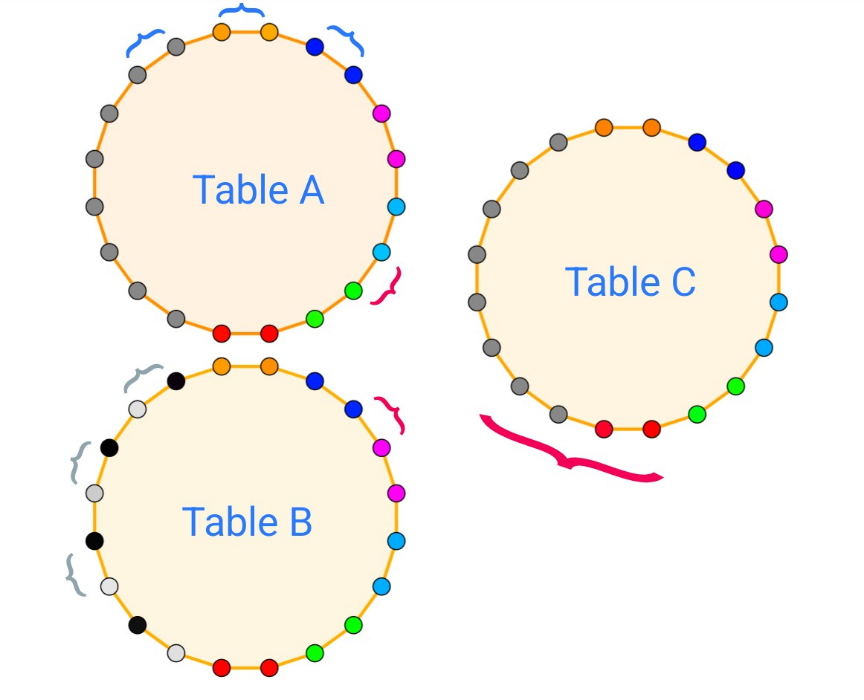
$${I}\:{try}\:{an}\:{answer}\:\left({figure}\:{follows}\right). \\ $$$$\mathrm{10}\:{couples}\:{are}\:\mathrm{20}\:{persons}. \\ $$$$\left.\mathrm{1}\right)\:{Arrangements}\:{of}\:\mathrm{20}\:{people},\:{even}\:{in} \\ $$$${circle},\:{with}\:{different}\:{places}\:{are}\:\mathrm{20}! \\ $$$$\left.\mathrm{2}\right)\:{Couples}\:{must}\:{sit}\:{in}\:{adjacent}\:{places}. \\ $$$${Consider}\:\mathrm{10}\:{twin}\:{seats}\:\left({see}\:{Table}\:{A}\right). \\ $$$${There}\:{are}\:\mathrm{10}!\:{ways}\:{for}\:\mathrm{10}\:{couples}. \\ $$$${Also},\:{couple}\:\mathrm{1}\:{can}\:{interchange}\:{seats} \\ $$$$\left(×\mathrm{2}\right),\:{couple}\:\mathrm{2}\:{can}\:{do}\:{the}\:{same}\:\left(×\mathrm{2}\right),... \\ $$$${till}\:{couple}\:\mathrm{10}\:\left(×\mathrm{2}\right),\:{e}.{g}.\:\mathrm{2}^{\mathrm{10}} .\:{Also},\:{all} \\ $$$${couples}\:{can}\:{shift}\:{one}\:{place}\:\left({see}\:{red}\right. \\ $$$$\left.{bracket}\right)\:\left(×\mathrm{2}\right).\:{Total}\:\mathrm{10}!\centerdot\mathrm{2}^{\mathrm{11}} \\ $$$$\left.\mathrm{3}\right)\:\left({suppose}\:{restriction}\:#\mathrm{2}\:{plus}...\right)\: \\ $$$$...{No}\:{two}\:{men}\:{in}\:{adjacent}\:{places}. \\ $$$${If}\:{the}\:{pattern}\:\left({mw}−{mw}−{mw}−{mw}...\right) \\ $$$$\left\{{where}\:{m}\:{man},\:{w}\:{woman}\right\}\:{changes}\:{to} \\ $$$$\left({mw}−{wm}−{wm}−{wm}...\right)\:{the}\:{circle} \\ $$$${doesn}'{t}\:{close}\:{normally}. \\ $$$$\mathrm{10}\:{couples}\:{are}\:{sitting}\:{in}\:\mathrm{10}\:{twin}\:{seats} \\ $$$${in}\:\mathrm{10}!\:{ways}\:\left({see}\:{Table}\:{B}\right).\:{Also},\:{the} \\ $$$${pattern}\:{can}\:{change}\:{to}\:\left({wm}−{wm}−{wm}...\right)\: \\ $$$$\left(×\mathrm{2}\right).\:{Also},\:{all}\:{couples}\:{can}\:{shift}\:{one} \\ $$$${place}\:\left({red}\:{bracket}\right)\:\left(×\mathrm{2}\right).\:{Total}\:\mathrm{10}!\centerdot\mathrm{2}^{\mathrm{2}} \\ $$$$\left.\mathrm{4}\right)\:{Restriction}\:\left(\mathrm{3}\right)\:{plus}\:{not}\:{two}\:{certain} \\ $$$${couples}\:{next}\:{to}\:{each}\:{other}. \\ $$$${Consider}\:{two}\:{couples},\:{red}\:{and}\:{blue},\:{not} \\ $$$${allowed}\:{in}\:{adjacent}\:{seats}\:\left({see}\:{Table}\:{C}\right). \\ $$$${Positions}\:\boldsymbol{{not}}\:{allowed}\:{for}\:{those}\:{two} \\ $$$${couples}\:{are}\:\mathrm{10}−\mathrm{1}\:\left(^{{a}} \right).\:{Remaining}\:\mathrm{8} \\ $$$${couples}\:{are}\:{sitted}\:{in}\:\mathrm{8}!\:{ways}\:\left(^{{b}} \right).\:{Also} \\ $$$${these}\:{two}\:{couples}\:{are}\:{not}\:{allowed}\:{at} \\ $$$${first}\:{and}\:{last}\:{positions},\:{where}\:{table} \\ $$$${ends}\:\left({see}\:{red}\:{bracket}\right),\:{so}\:{remaining} \\ $$$$\mathrm{8}\:{couples}\:{have}\:{another}\:\mathrm{8}!\:{ways}\:{of} \\ $$$${sitting}\:\left(^{{c}} \right).\:{Also},\:{couples}\:{can} \\ $$$${interchange}\:{seats}\:×\mathrm{2}\:\left(^{{d}} \right). \\ $$$${Knowing}\:{all}\:{arrangements}\:{are}\:\mathrm{10}!, \\ $$$${above}\:{exceptions}\:{are}\:{deducted}. \\ $$$$\mathrm{10}!−\underset{{d}} {\underbrace{\mathrm{2}}}\centerdot\underset{{a}} {\underbrace{\left(\mathrm{10}−\mathrm{1}\right)}\underset{{b}} {\left(\mathrm{10}−\mathrm{2}\right)!}}−\underset{{d}} {\underbrace{\mathrm{2}}}\centerdot\underset{{c}} {\underbrace{\left(\mathrm{10}−\mathrm{2}\right)!}}= \\ $$$$\mathrm{10}!−\left(\mathrm{10}−\mathrm{2}\right)!\left[\mathrm{2}\left(\mathrm{10}−\mathrm{1}\right)+\mathrm{2}\right]= \\ $$$$\mathrm{10}!−\mathrm{2}\centerdot\mathrm{10}\left(\mathrm{10}−\mathrm{2}\right)!=\mathrm{10}\centerdot\left(\mathrm{10}−\mathrm{3}\right)\left(\mathrm{10}−\mathrm{2}\right)! \\ $$$${Finally},\:{cases}\:{allowed}\:{must}\:×\mathrm{2}\:{for} \\ $$$${interchanging}\:{seats},\:×\mathrm{2}\:{for}\:{shifting} \\ $$$${one}\:{place}.\:{Total}\:\mathrm{8}!\centerdot\mathrm{10}\centerdot\mathrm{7}\centerdot\mathrm{2}^{\mathrm{2}} \\ $$
Commented by nikif99 last updated on 08/Apr/25
Commented by mr W last updated on 19/Apr/25

$${thanks}! \\ $$$${we}\:{should}\:{consider}\:{that}\:{the}\:{table} \\ $$$${is}\:{round}\:{and}\:{the}\:{seats}\:{are}\:{identical}. \\ $$$$ \\ $$$$\left.{as}\:{for}\:\mathrm{4}\right)\:{let}'{s}\:{look}\:{at}\:{the}\:{case}\:{with} \\ $$$${only}\:\mathrm{4}\:{couples}.\:{i}'{ll}\:{get} \\ $$$$\mathrm{4}!×\mathrm{3}!−\mathrm{2}×\mathrm{2}×\mathrm{3}!×\mathrm{3}!+\mathrm{2}×\mathrm{2}!×\mathrm{3}!=\mathrm{24}. \\ $$$${it}\:{should}\:{be}\:{able}\:{to}\:{check}\:{this} \\ $$$${manuelly}. \\ $$
Answered by mr W last updated on 19/Apr/25

$$\left.\mathrm{1}\right) \\ $$$${arrange}\:\mathrm{20}\:{persons}\:{around}\:{round} \\ $$$${table}: \\ $$$$\left(\mathrm{20}−\mathrm{1}\right)!=\mathrm{19}! \\ $$$$ \\ $$$$\left.\mathrm{2}\right) \\ $$$${arrange}\:\mathrm{10}\:{couples}\:{around}\:{round} \\ $$$${table},\:{there}\:{are}\:\left(\mathrm{10}−\mathrm{1}\right)!\:{ways}.\:{each} \\ $$$${couple}\:{has}\:\mathrm{2}\:{ways}\:{to}\:{change}\:{the} \\ $$$${positions}\:{of}\:{husband}\:{and}\:{wife}: \\ $$$$\left(\mathrm{10}−\mathrm{1}\right)!×\mathrm{2}^{\mathrm{10}} =\mathrm{9}!×\mathrm{2}^{\mathrm{10}} \\ $$$$ \\ $$$$\left.\mathrm{3}\right) \\ $$$${to}\:{arrange}\:\mathrm{10}\:{wivesaround}\:{round} \\ $$$${table}\:{there}\:{are}\:\left(\mathrm{10}−\mathrm{1}\right)!\:{ways}.\:{to} \\ $$$${arrange}\:{the}\:\mathrm{10}\:{husbands}\:{there}\:{are} \\ $$$$\mathrm{10}!\:{ways}: \\ $$$$\left(\mathrm{10}−\mathrm{1}\right)!×\mathrm{10}!=\mathrm{9}!×\mathrm{10}!=\mathrm{90}×\mathrm{8}!×\mathrm{9}! \\ $$$$ \\ $$$$\left.\mathrm{4}\right) \\ $$$$\mathrm{10}!×\mathrm{9}!−\mathrm{2}×\mathrm{2}×\mathrm{9}!×\mathrm{9}!+\mathrm{2}×\mathrm{8}!×\mathrm{9}! \\ $$$$=\mathrm{56}×\mathrm{8}!×\mathrm{9}! \\ $$
