Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 12107 by Joel576 last updated on 13/Apr/17

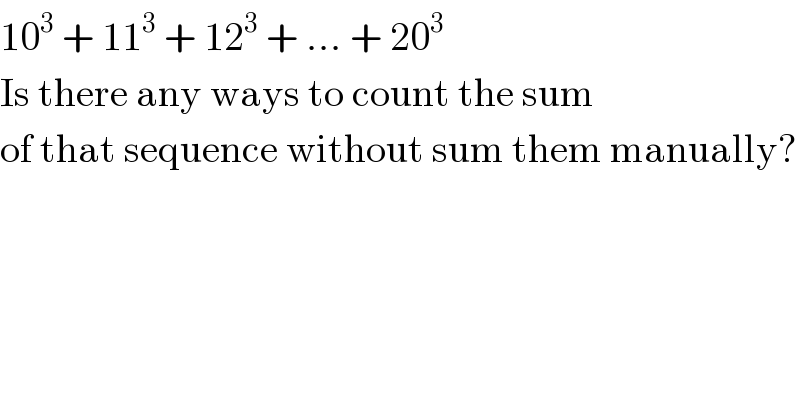
10^3 + 11^3 + 12^3 + ... + 20^3 Is there any ways to count the sum of that sequence without sum them manually?

$$\mathrm{10}^{\mathrm{3}} \:+\:\mathrm{11}^{\mathrm{3}} \:+\:\mathrm{12}^{\mathrm{3}} \:+\:...\:+\:\mathrm{20}^{\mathrm{3}} \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{count}\:\mathrm{the}\:\mathrm{sum}\: \\ $$$$\mathrm{of}\:\mathrm{that}\:\mathrm{sequence}\:\mathrm{without}\:\mathrm{sum}\:\mathrm{them}\:\mathrm{manually}? \\ $$

Commented by FilupS last updated on 13/Apr/17

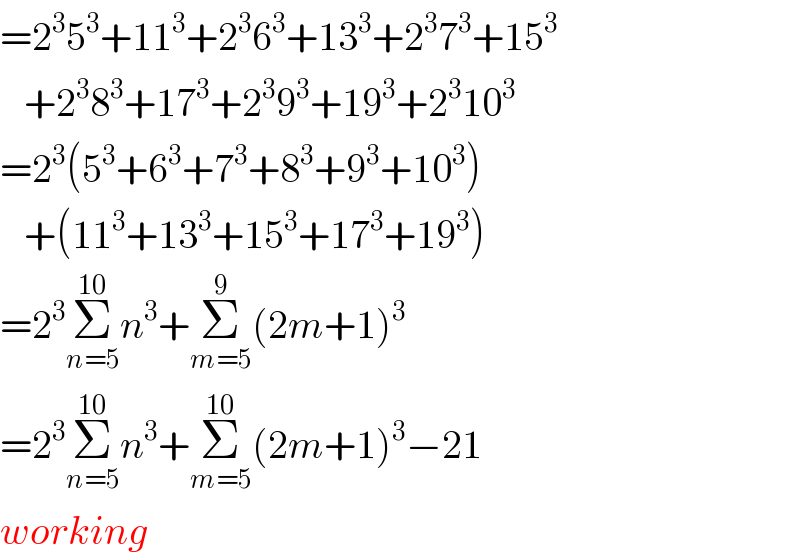
=2^3 5^3 +11^3 +2^3 6^3 +13^3 +2^3 7^3 +15^3 +2^3 8^3 +17^3 +2^3 9^3 +19^3 +2^3 10^3 =2^3 (5^3 +6^3 +7^3 +8^3 +9^3 +10^3 ) +(11^3 +13^3 +15^3 +17^3 +19^3 ) =2^3 Σ_(n=5) ^(10) n^3 +Σ_(m=5) ^9 (2m+1)^3 =2^3 Σ_(n=5) ^(10) n^3 +Σ_(m=5) ^(10) (2m+1)^3 −21 working

$$=\mathrm{2}^{\mathrm{3}} \mathrm{5}^{\mathrm{3}} +\mathrm{11}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{6}^{\mathrm{3}} +\mathrm{13}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{7}^{\mathrm{3}} +\mathrm{15}^{\mathrm{3}} \\ $$$$\:\:\:+\mathrm{2}^{\mathrm{3}} \mathrm{8}^{\mathrm{3}} +\mathrm{17}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{9}^{\mathrm{3}} +\mathrm{19}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} \mathrm{10}^{\mathrm{3}} \\ $$$$=\mathrm{2}^{\mathrm{3}} \left(\mathrm{5}^{\mathrm{3}} +\mathrm{6}^{\mathrm{3}} +\mathrm{7}^{\mathrm{3}} +\mathrm{8}^{\mathrm{3}} +\mathrm{9}^{\mathrm{3}} +\mathrm{10}^{\mathrm{3}} \right) \\ $$$$\:\:\:+\left(\mathrm{11}^{\mathrm{3}} +\mathrm{13}^{\mathrm{3}} +\mathrm{15}^{\mathrm{3}} +\mathrm{17}^{\mathrm{3}} +\mathrm{19}^{\mathrm{3}} \right) \\ $$$$=\mathrm{2}^{\mathrm{3}} \underset{{n}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}{n}^{\mathrm{3}} +\underset{{m}=\mathrm{5}} {\overset{\mathrm{9}} {\sum}}\left(\mathrm{2}{m}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$=\mathrm{2}^{\mathrm{3}} \underset{{n}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}{n}^{\mathrm{3}} +\underset{{m}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{2}{m}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{21} \\ $$$${working} \\ $$

Commented by Joel576 last updated on 14/Apr/17

but how to count [Σ_(m=5) ^(10) (2m + 1)^3 ] − 21^3 without adding them manually?

$$\mathrm{but}\:\mathrm{how}\:\mathrm{to}\:\mathrm{count}\:\left[\underset{{m}=\mathrm{5}} {\overset{\mathrm{10}} {\sum}}\left(\mathrm{2}{m}\:+\:\mathrm{1}\right)^{\mathrm{3}} \right]\:−\:\mathrm{21}^{\mathrm{3}} \\ $$$$\mathrm{without}\:\mathrm{adding}\:\mathrm{them}\:\mathrm{manually}? \\ $$

Answered by mrW1 last updated on 13/Apr/17

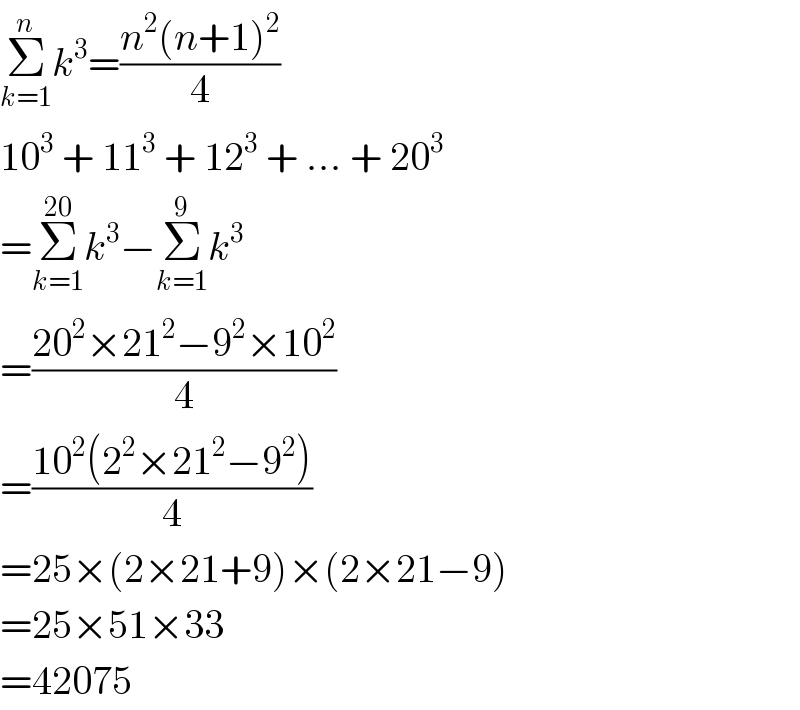
Σ_(k=1) ^n k^3 =((n^2 (n+1)^2 )/4) 10^3 + 11^3 + 12^3 + ... + 20^3 =Σ_(k=1) ^(20) k^3 −Σ_(k=1) ^9 k^3 =((20^2 ×21^2 −9^2 ×10^2 )/4) =((10^2 (2^2 ×21^2 −9^2 ))/4) =25×(2×21+9)×(2×21−9) =25×51×33 =42075

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} =\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{10}^{\mathrm{3}} \:+\:\mathrm{11}^{\mathrm{3}} \:+\:\mathrm{12}^{\mathrm{3}} \:+\:...\:+\:\mathrm{20}^{\mathrm{3}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}{k}^{\mathrm{3}} −\underset{{k}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}{k}^{\mathrm{3}} \\ $$$$=\frac{\mathrm{20}^{\mathrm{2}} ×\mathrm{21}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} ×\mathrm{10}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\mathrm{10}^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} ×\mathrm{21}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \right)}{\mathrm{4}} \\ $$$$=\mathrm{25}×\left(\mathrm{2}×\mathrm{21}+\mathrm{9}\right)×\left(\mathrm{2}×\mathrm{21}−\mathrm{9}\right) \\ $$$$=\mathrm{25}×\mathrm{51}×\mathrm{33} \\ $$$$=\mathrm{42075} \\ $$

Commented by Joel576 last updated on 14/Apr/17

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com