Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 143184 by bramlexs22 last updated on 11/Jun/21

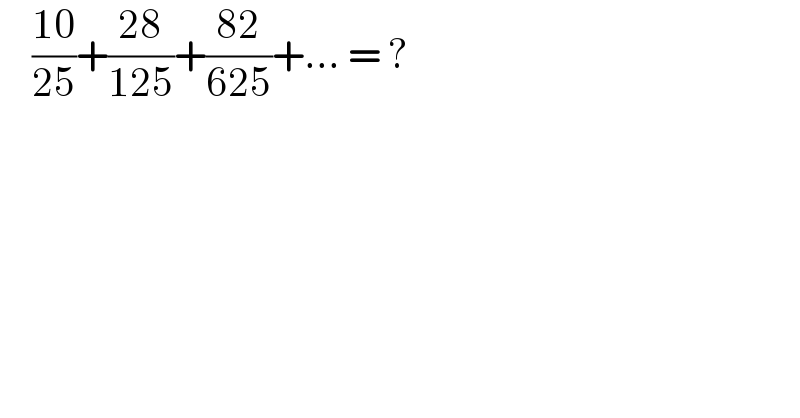
((10)/(25))+((28)/(125))+((82)/(625))+... = ?

$$\:\:\:\:\frac{\mathrm{10}}{\mathrm{25}}+\frac{\mathrm{28}}{\mathrm{125}}+\frac{\mathrm{82}}{\mathrm{625}}+...\:=\:? \\ $$

Answered by Canebulok last updated on 11/Jun/21

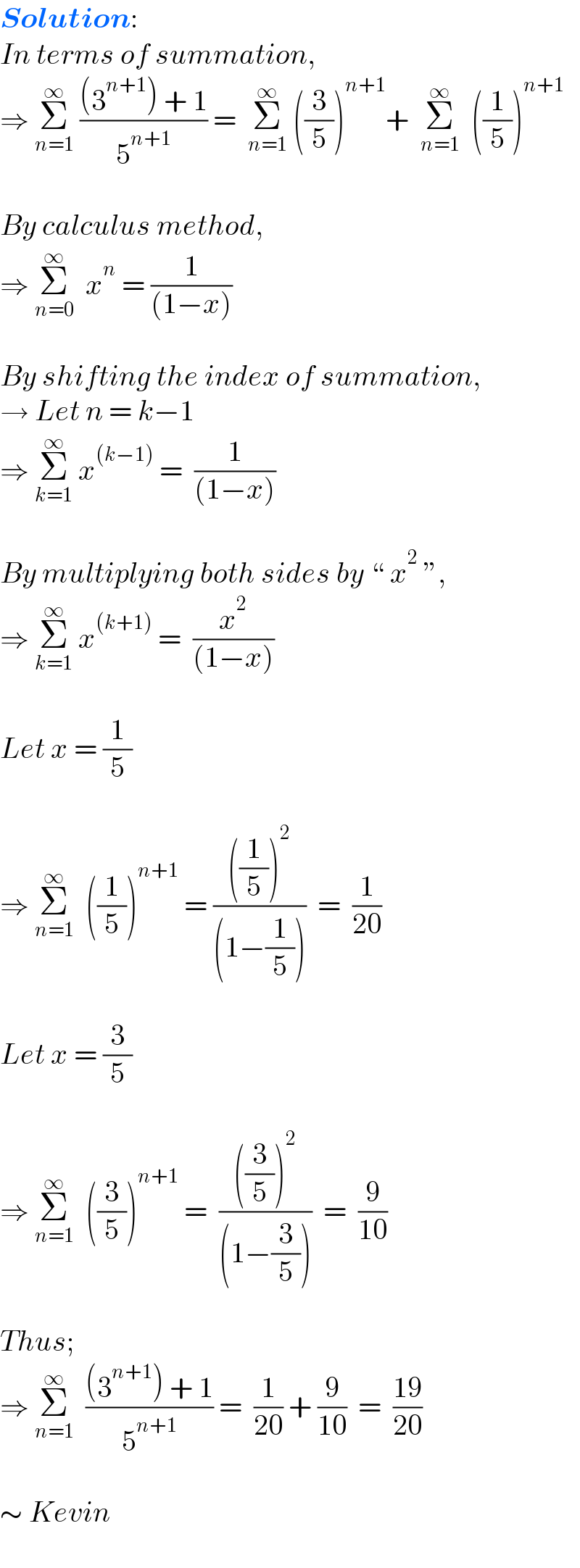
Solution: In terms of summation, ⇒ Σ_(n=1) ^∞ (((3^(n+1) ) + 1)/5^(n+1) ) = Σ_(n=1) ^∞ ((3/5))^(n+1) + Σ_(n=1) ^∞ ((1/5))^(n+1) By calculus method, ⇒ Σ_(n=0) ^∞ x^n = (1/((1−x))) By shifting the index of summation, → Let n = k−1 ⇒ Σ_(k=1) ^∞ x^((k−1)) = (1/((1−x))) By multiplying both sides by “ x^2 ”, ⇒ Σ_(k=1) ^∞ x^((k+1)) = (x^2 /((1−x))) Let x = (1/5) ⇒ Σ_(n=1) ^∞ ((1/5))^(n+1) = ((((1/5))^2 )/((1−(1/5)))) = (1/(20)) Let x = (3/5) ⇒ Σ_(n=1) ^∞ ((3/5))^(n+1) = ((((3/5))^2 )/((1−(3/5)))) = (9/(10)) Thus; ⇒ Σ_(n=1) ^∞ (((3^(n+1) ) + 1)/5^(n+1) ) = (1/(20)) + (9/(10)) = ((19)/(20)) ∼ Kevin

$$\boldsymbol{{Solution}}: \\ $$$${In}\:{terms}\:{of}\:{summation}, \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(\mathrm{3}^{{n}+\mathrm{1}} \right)\:+\:\mathrm{1}}{\mathrm{5}^{{n}+\mathrm{1}} }\:=\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}+\mathrm{1}} +\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}+\mathrm{1}} \: \\ $$$$\: \\ $$$${By}\:{calculus}\:{method}, \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\:{x}^{{n}} \:=\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)} \\ $$$$\: \\ $$$${By}\:{shifting}\:{the}\:{index}\:{of}\:{summation}, \\ $$$$\rightarrow\:{Let}\:{n}\:=\:{k}−\mathrm{1} \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:{x}^{\left({k}−\mathrm{1}\right)} \:=\:\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)} \\ $$$$\: \\ $$$${By}\:{multiplying}\:{both}\:{sides}\:{by}\:``\:{x}^{\mathrm{2}} \:'', \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:{x}^{\left({k}+\mathrm{1}\right)} \:=\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)} \\ $$$$\: \\ $$$${Let}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\: \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}+\mathrm{1}} \:=\:\frac{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right)}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{20}} \\ $$$$\: \\ $$$${Let}\:{x}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\: \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{n}+\mathrm{1}} \:=\:\:\frac{\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}\right)}\:\:=\:\:\frac{\mathrm{9}}{\mathrm{10}} \\ $$$$\: \\ $$$${Thus}; \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{\left(\mathrm{3}^{{n}+\mathrm{1}} \right)\:+\:\mathrm{1}}{\mathrm{5}^{{n}+\mathrm{1}} }\:=\:\:\frac{\mathrm{1}}{\mathrm{20}}\:+\:\frac{\mathrm{9}}{\mathrm{10}}\:\:=\:\:\frac{\mathrm{19}}{\mathrm{20}} \\ $$$$\: \\ $$$$\sim\:{Kevin} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com