Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 195443 by MM42 last updated on 02/Aug/23

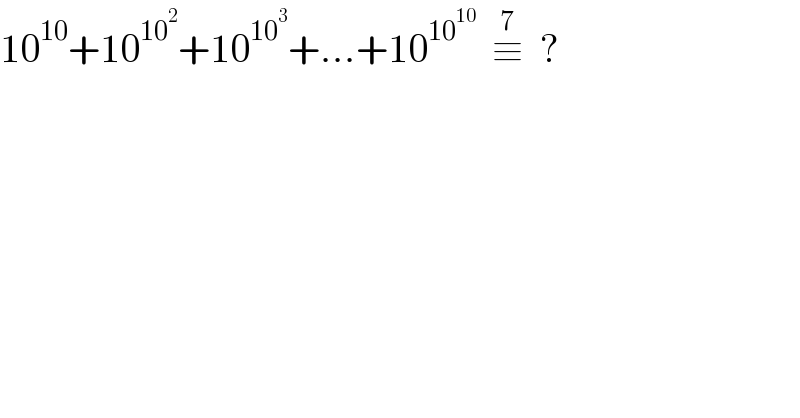
10^(10) +10^(10^2 ) +10^(10^3 ) +...+10^(10^(10) ) ≡^7 ?

$$\mathrm{10}^{\mathrm{10}} +\mathrm{10}^{\mathrm{10}^{\mathrm{2}} } +\mathrm{10}^{\mathrm{10}^{\mathrm{3}} } +...+\mathrm{10}^{\mathrm{10}^{\mathrm{10}} } \:\:\overset{\mathrm{7}} {\equiv}\:\:? \\ $$

Answered by BaliramKumar last updated on 02/Aug/23

5

$$\mathrm{5} \\ $$

Commented by MM42 last updated on 02/Aug/23

ok

$${ok} \\ $$

Answered by BaliramKumar last updated on 02/Aug/23

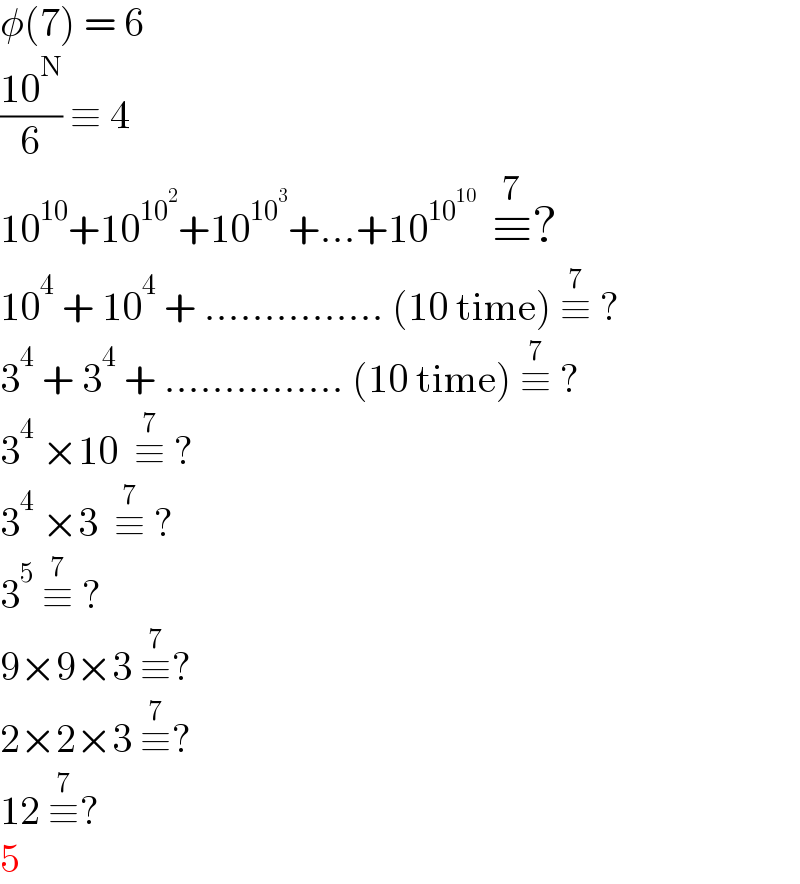
φ(7) = 6 ((10^N )/6) ≡ 4 10^(10) +10^(10^2 ) +10^(10^3 ) +...+10^(10^(10) ) ≡^7 ? 10^4 + 10^4 + ............... (10 time) ≡^7 ? 3^4 + 3^4 + ............... (10 time) ≡^7 ? 3^4 ×10 ≡^7 ? 3^4 ×3 ≡^7 ? 3^5 ≡^7 ? 9×9×3 ≡^7 ? 2×2×3 ≡^7 ? 12 ≡^7 ? 5

$$\phi\left(\mathrm{7}\right)\:=\:\mathrm{6} \\ $$$$\frac{\mathrm{10}^{\mathrm{N}} }{\mathrm{6}}\:\equiv\:\mathrm{4} \\ $$$$\mathrm{10}^{\mathrm{10}} +\mathrm{10}^{\mathrm{10}^{\mathrm{2}} } +\mathrm{10}^{\mathrm{10}^{\mathrm{3}} } +...+\mathrm{10}^{\mathrm{10}^{\mathrm{10}} } \:\:\overset{\mathrm{7}} {\equiv}? \\ $$$$\mathrm{10}^{\mathrm{4}} \:+\:\mathrm{10}^{\mathrm{4}} \:+\:...............\:\left(\mathrm{10}\:\mathrm{time}\right)\:\overset{\mathrm{7}} {\equiv}\:? \\ $$$$\mathrm{3}^{\mathrm{4}} \:+\:\mathrm{3}^{\mathrm{4}} \:+\:...............\:\left(\mathrm{10}\:\mathrm{time}\right)\:\overset{\mathrm{7}} {\equiv}\:? \\ $$$$\mathrm{3}^{\mathrm{4}} \:×\mathrm{10}\:\:\overset{\mathrm{7}} {\equiv}\:? \\ $$$$\mathrm{3}^{\mathrm{4}} \:×\mathrm{3}\:\:\overset{\mathrm{7}} {\equiv}\:? \\ $$$$\mathrm{3}^{\mathrm{5}} \:\overset{\mathrm{7}} {\equiv}\:? \\ $$$$\mathrm{9}×\mathrm{9}×\mathrm{3}\:\overset{\mathrm{7}} {\equiv}? \\ $$$$\mathrm{2}×\mathrm{2}×\mathrm{3}\:\overset{\mathrm{7}} {\equiv}? \\ $$$$\mathrm{12}\:\overset{\mathrm{7}} {\equiv}? \\ $$$$\mathrm{5} \\ $$

Commented by MM42 last updated on 03/Aug/23

your solution was beautiful another solution 10^n =3k+1 ; “k” is odd. 10≡_7 3 10^(10) +10^(10^2 ) +10^(10^3 ) +...+10^(10^(10) ) ≡_7 3^(10) +3^(10^2 ) +3^(10^3 ) +...+3^(10^(10) ) =3^(3k_1 +1) +3^(3k_2 +1) +3^(3k_3 +1) +...+3^(3k_(10) +1) ; “k_i ” is odd =3×(27)^k_1 +3×(27)^k_2 +3×(27)^k_3 +...+3×(27)^k_(10) ≡_7 −3−3−3−...−3=−30≡_7 5

$${your}\:{solution}\:{was}\:{beautiful} \\ $$$${another}\:{solution} \\ $$$$\mathrm{10}^{{n}} =\mathrm{3}{k}+\mathrm{1}\:\:;\:``{k}''\:{is}\:{odd}. \\ $$$$\mathrm{10}\underset{\mathrm{7}} {\equiv}\mathrm{3} \\ $$$$\mathrm{10}^{\mathrm{10}} +\mathrm{10}^{\mathrm{10}^{\mathrm{2}} } +\mathrm{10}^{\mathrm{10}^{\mathrm{3}} } +...+\mathrm{10}^{\mathrm{10}^{\mathrm{10}} } \\ $$$$\underset{\mathrm{7}} {\equiv}\mathrm{3}^{\mathrm{10}} +\mathrm{3}^{\mathrm{10}^{\mathrm{2}} } +\mathrm{3}^{\mathrm{10}^{\mathrm{3}} } +...+\mathrm{3}^{\mathrm{10}^{\mathrm{10}} } \\ $$$$=\mathrm{3}^{\mathrm{3}{k}_{\mathrm{1}} +\mathrm{1}} +\mathrm{3}^{\mathrm{3}{k}_{\mathrm{2}} +\mathrm{1}} +\mathrm{3}^{\mathrm{3}{k}_{\mathrm{3}} +\mathrm{1}} +...+\mathrm{3}^{\mathrm{3}{k}_{\mathrm{10}} +\mathrm{1}} \:\:\:\:;\:``{k}_{{i}} ''\:\:{is}\:\:{odd} \\ $$$$=\mathrm{3}×\left(\mathrm{27}\right)^{{k}_{\mathrm{1}} } +\mathrm{3}×\left(\mathrm{27}\right)^{{k}_{\mathrm{2}} } +\mathrm{3}×\left(\mathrm{27}\right)^{{k}_{\mathrm{3}} } +...+\mathrm{3}×\left(\mathrm{27}\right)^{{k}_{\mathrm{10}} } \\ $$$$\underset{\mathrm{7}} {\equiv}−\mathrm{3}−\mathrm{3}−\mathrm{3}−...−\mathrm{3}=−\mathrm{30}\underset{\mathrm{7}} {\equiv}\:\mathrm{5} \\ $$$$\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com