
Question Number 170206 by bounhome last updated on 18/May/22
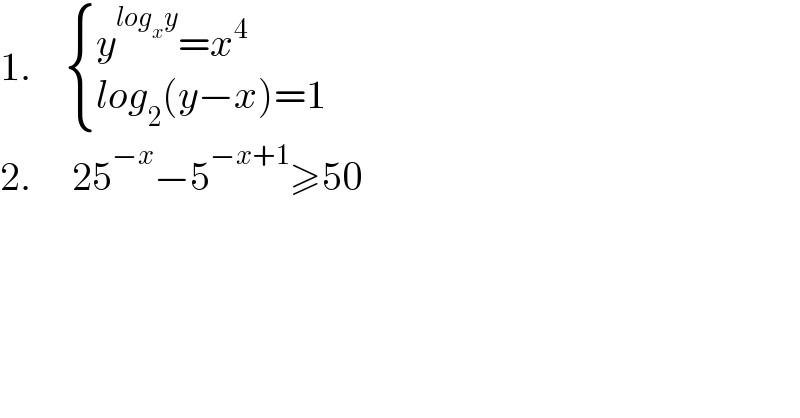
$$\mathrm{1}.\:\:\:\:\begin{cases}{{y}^{{log}_{{x}} {y}} ={x}^{\mathrm{4}} }\\{{log}_{\mathrm{2}} \left({y}−{x}\right)=\mathrm{1}}\end{cases} \\ $$$$\mathrm{2}.\:\:\:\:\:\mathrm{25}^{−{x}} −\mathrm{5}^{−{x}+\mathrm{1}} \geqslant\mathrm{50} \\ $$
Answered by aleks041103 last updated on 18/May/22
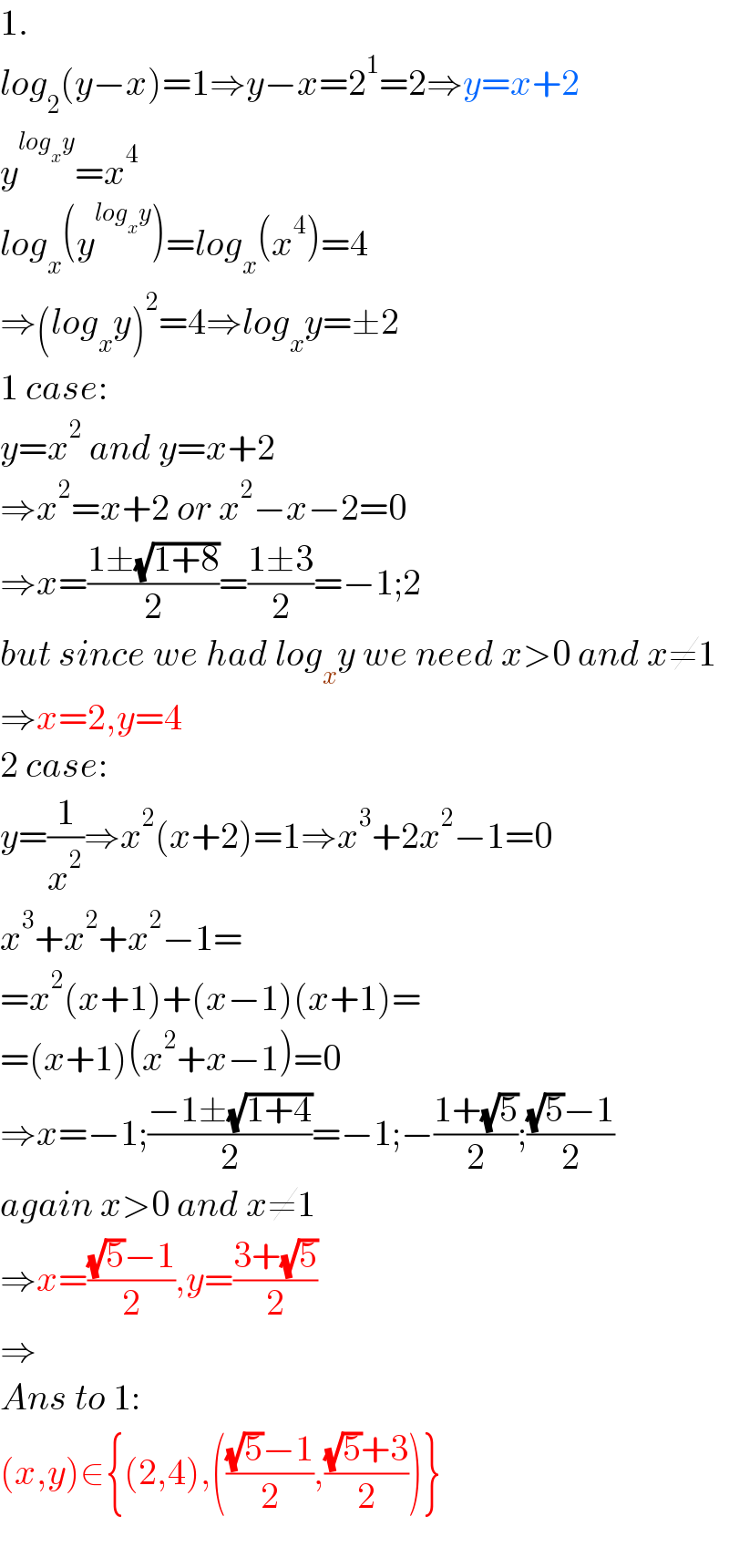
$$\mathrm{1}. \\ $$$${log}_{\mathrm{2}} \left({y}−{x}\right)=\mathrm{1}\Rightarrow{y}−{x}=\mathrm{2}^{\mathrm{1}} =\mathrm{2}\Rightarrow{y}={x}+\mathrm{2} \\ $$$${y}^{{log}_{{x}} {y}} ={x}^{\mathrm{4}} \\ $$$${log}_{{x}} \left({y}^{{log}_{{x}} {y}} \right)={log}_{{x}} \left({x}^{\mathrm{4}} \right)=\mathrm{4} \\ $$$$\Rightarrow\left({log}_{{x}} {y}\right)^{\mathrm{2}} =\mathrm{4}\Rightarrow{log}_{{x}} {y}=\pm\mathrm{2} \\ $$$$\mathrm{1}\:{case}: \\ $$$${y}={x}^{\mathrm{2}} \:{and}\:{y}={x}+\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} ={x}+\mathrm{2}\:{or}\:{x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{8}}}{\mathrm{2}}=\frac{\mathrm{1}\pm\mathrm{3}}{\mathrm{2}}=−\mathrm{1};\mathrm{2} \\ $$$${but}\:{since}\:{we}\:{had}\:{log}_{{x}} {y}\:{we}\:{need}\:{x}>\mathrm{0}\:{and}\:{x}\neq\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{2},{y}=\mathrm{4} \\ $$$$\mathrm{2}\:{case}: \\ $$$${y}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\Rightarrow{x}^{\mathrm{2}} \left({x}+\mathrm{2}\right)=\mathrm{1}\Rightarrow{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{1}= \\ $$$$={x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)= \\ $$$$=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{1};\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=−\mathrm{1};−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}};\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$${again}\:{x}>\mathrm{0}\:{and}\:{x}\neq\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}},{y}=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${Ans}\:{to}\:\mathrm{1}: \\ $$$$\left({x},{y}\right)\in\left\{\left(\mathrm{2},\mathrm{4}\right),\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}},\frac{\sqrt{\mathrm{5}}+\mathrm{3}}{\mathrm{2}}\right)\right\} \\ $$$$ \\ $$
Answered by aleks041103 last updated on 18/May/22
![2. 25^(−x) −5^(−x+1) =(5^(−x) )^2 −5(5^(−x) ) let t=5^(−x) ⇒t∈(0,∞) ⇒t^2 −5t≥50 ⇒t^2 −5t−50≥0 t_(1,2) =((5±(√(25+200)))/2)=((5±15)/2)=−5,10 ⇒t^2 −5t−50≥0 for t∈(−∞,−5]∪[10,+∞) ⇒t∈{(−∞,−5]∪[10,+∞)}∩(0,∞) ⇒t∈[10,∞) ⇒5^(−x) ∈[10,∞) ⇒−x∈[log_5 10,∞)=[1+log_5 2,∞) ⇒x∈(−∞,−1−log_5 2] ⇒Ans. x≤−1−log_5 2](Q170220.png)
$$\mathrm{2}. \\ $$$$\mathrm{25}^{−{x}} −\mathrm{5}^{−{x}+\mathrm{1}} =\left(\mathrm{5}^{−{x}} \right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{5}^{−{x}} \right) \\ $$$${let}\:{t}=\mathrm{5}^{−{x}} \Rightarrow{t}\in\left(\mathrm{0},\infty\right) \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{5}{t}\geqslant\mathrm{50} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{5}{t}−\mathrm{50}\geqslant\mathrm{0} \\ $$$${t}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{25}+\mathrm{200}}}{\mathrm{2}}=\frac{\mathrm{5}\pm\mathrm{15}}{\mathrm{2}}=−\mathrm{5},\mathrm{10} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{5}{t}−\mathrm{50}\geqslant\mathrm{0}\:{for}\:{t}\in\left(−\infty,−\mathrm{5}\right]\cup\left[\mathrm{10},+\infty\right) \\ $$$$\Rightarrow{t}\in\left\{\left(−\infty,−\mathrm{5}\right]\cup\left[\mathrm{10},+\infty\right)\right\}\cap\left(\mathrm{0},\infty\right) \\ $$$$\Rightarrow{t}\in\left[\mathrm{10},\infty\right) \\ $$$$\Rightarrow\mathrm{5}^{−{x}} \in\left[\mathrm{10},\infty\right) \\ $$$$\Rightarrow−{x}\in\left[{log}_{\mathrm{5}} \mathrm{10},\infty\right)=\left[\mathrm{1}+{log}_{\mathrm{5}} \mathrm{2},\infty\right) \\ $$$$\Rightarrow{x}\in\left(−\infty,−\mathrm{1}−{log}_{\mathrm{5}} \mathrm{2}\right] \\ $$$$\Rightarrow{Ans}.\:{x}\leqslant−\mathrm{1}−{log}_{\mathrm{5}} \mathrm{2} \\ $$
