
Question Number 205200 by mathlove last updated on 12/Mar/24
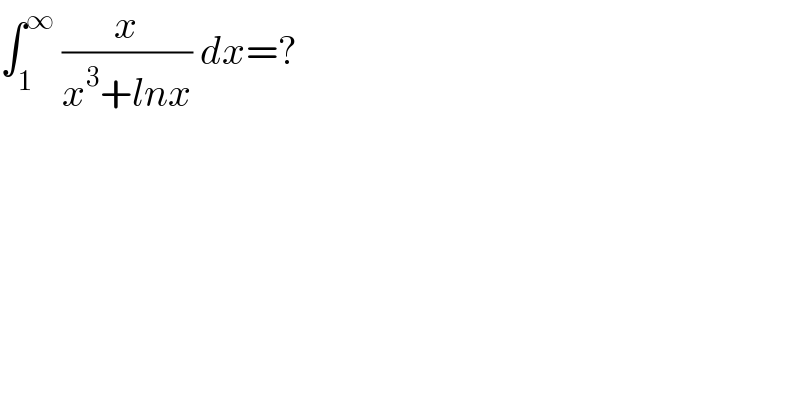
$$\int_{\mathrm{1}} ^{\infty} \:\frac{{x}}{{x}^{\mathrm{3}} +{lnx}}\:{dx}=? \\ $$
Answered by mathzup last updated on 12/Mar/24
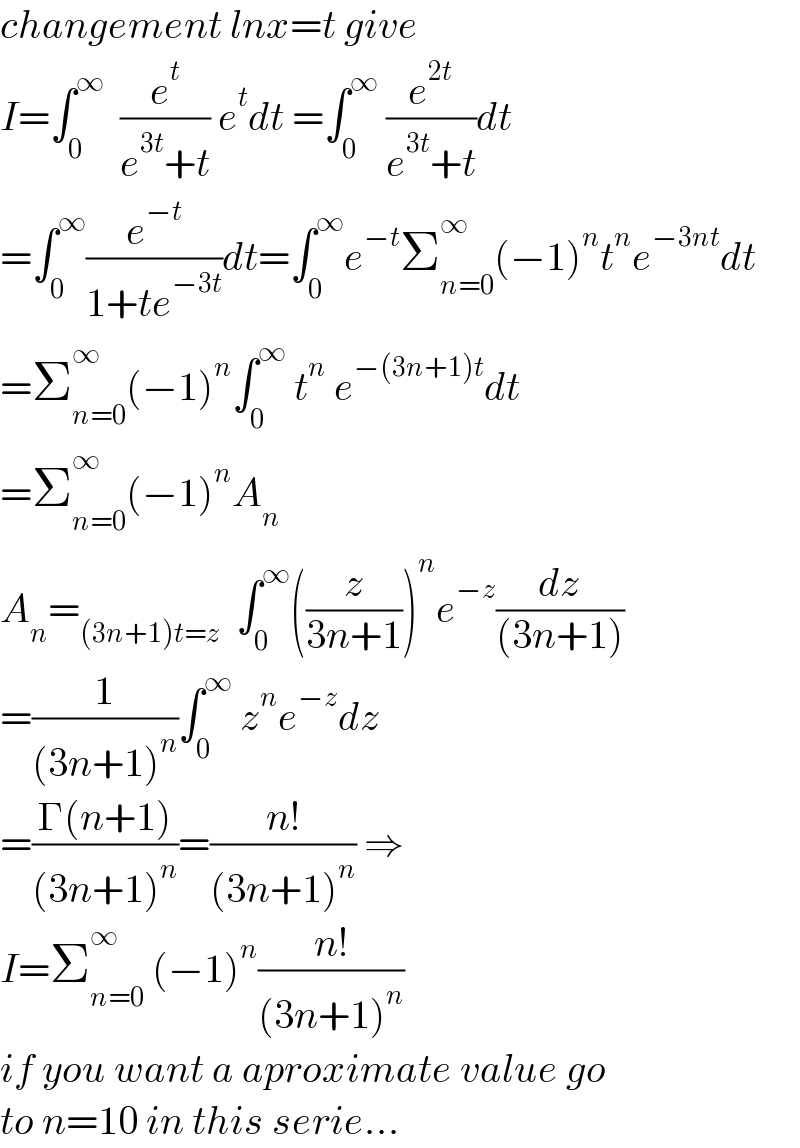
$${changement}\:{lnx}={t}\:{give} \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{{t}} }{{e}^{\mathrm{3}{t}} +{t}}\:{e}^{{t}} {dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{\mathrm{2}{t}} }{{e}^{\mathrm{3}{t}} +{t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{\mathrm{1}+{te}^{−\mathrm{3}{t}} }{dt}=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} \sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}} {e}^{−\mathrm{3}{nt}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−\left(\mathrm{3}{n}+\mathrm{1}\right){t}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {A}_{{n}} \\ $$$${A}_{{n}} =_{\left(\mathrm{3}{n}+\mathrm{1}\right){t}={z}} \:\:\int_{\mathrm{0}} ^{\infty} \left(\frac{{z}}{\mathrm{3}{n}+\mathrm{1}}\right)^{{n}} {e}^{−{z}} \frac{{dz}}{\left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{{n}} }\int_{\mathrm{0}} ^{\infty} \:{z}^{{n}} {e}^{−{z}} {dz} \\ $$$$=\frac{\Gamma\left({n}+\mathrm{1}\right)}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{{n}} }=\frac{{n}!}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{{n}} }\:\Rightarrow \\ $$$${I}=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \frac{{n}!}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{{n}} } \\ $$$${if}\:{you}\:{want}\:{a}\:{aproximate}\:{value}\:{go} \\ $$$${to}\:{n}=\mathrm{10}\:{in}\:{this}\:{serie}... \\ $$
